- Eşkenar Üçgen - 05/05/2017
- İntegral - 01/04/2016
- İntegral - 10/05/2015
- Kareler 06/01/2015
- Labirent 12/07/2014
- Elips ve Teğetleri 04/07/2014
- İntegral 20/06/2014
- Elips içinde üçgen 28/03/2014
- Mutlak Değer 20/03/2014
- Çemberlere Eşit Uzaklık 03/03/2014
- Köyler arası yollar 23/02/2014
- Ardışık yazılımlar 16/02/2014
- Kombinasyon Özdeşliği 10/02/2014
- Üç kişinin buluşması 25/01/2014
- Parabolün dik teğetleri 05/01/2014
- Bir açı sorusu 24/11/2013
- Alt küme elemanlar çarpımı 07/11/2013
- Kare ve Çemberler 30/10/2013
- Bir cebir sorusu 30/10/2013
- Dörtgen oluşturma olasılığı 01/06/2013
Soru
\[y = a{x^2} + bx + c\] parabolünün dik kesişen teğetlerinin kesim noktalarının geometrik yerinin \[y = - \dfrac{{\Delta + 1}}{{4a}}\] olduğunu gösteriniz.
Çözüm
Verilen parabolün dik kesişine teğetlerinden rastgele ikisinin kesiştiği nokta \(P(x_0,y_0)\) olsun. Bu teğetlerin eğimlerine sırasıyla \({m_1}\) ve \({m_2}\) diyelim. Bu durumda teğetlerin denklemleri sırasıyla \[y = {m_1}(x - {x_0}) + {y_0}\] ve \[y = {m_2}(x - {x_0}) + {y_0}\] olacaktır. Biz eğimlere genel olarak \(m\) diyerek her iki teğeti de kapsayan \[y = m(x - {x_0}) + {y_0}\] denklemini yazalım. Teğetler ile parabolün kesim noktası tek olduğundan, bu denklem ile parabolün denkleminin ortak çözümünden elde edilecek olan 2. dereceden bir bilinmeyenli denklemin tek kökü yani diskriminantı 0 a eşit olmalıdır: \[\begin{array}{*{20}{c}} {m(x - {x_0}) + {y_0} = a{x^2} + bx + c}\\ { \Rightarrow a{x^2} + x(b - m) + c + m{x_0} - {y_0} = 0} \end{array}\] olacağından \[\begin{array}{l} \Delta = {(b - m)^2} - 4a(c + m{x_0} - {y_0}) = 0\\ \Rightarrow {m^2} + m( - 2b - 4a{x_0}) + {b^2} - 4ac + 4a{y_0} = 0 \end{array}\] elde edilir. Elde edilen \(m\) ye bağlı bu 2.dereceden denklemden elde edilecek olan \({m_1}\) ve \({m_2}\) kökleri teğetlerin eğimleri olacaktır. Fakat biliyoruz ki teğetler dik kesişmektedir. O halde \[{m_1} \cdot {m_2} = - 1\] dir. Bu durumda elde ettiğimiz \(m\) ye bağlı bu 2.dereceden denklemde \[\begin{array}{l} \dfrac{c}{a} = - 1\\ \Rightarrow \dfrac{{{b^2} - 4ac + 4a{y_0}}}{1} = - 1\\ \Rightarrow \Delta + 4a{y_0} = - 1\\ \Rightarrow {y_0} = - \dfrac{{\Delta + 1}}{{4a}} \end{array}\] elde edilir. O halde dik kesişen teğetlerin kesim noktasının ordinatı daima bu değere eşittir. Demek ki bu noktalar \[y = - \dfrac{{\Delta + 1}}{{4a}}\] doğrusu üzerindedir.
Böylece ispat tamamlanmış olur.
Şimdi, parabolün denklemi genel konik denklemine dönüştürelim. \[\begin{array}{l}
y = a\left[ {{x^2} + \dfrac{b}{a}x + \dfrac{c}{a}} \right]\\ \Rightarrow y = a\left[ {{x^2} + \dfrac{b}{a}x + \dfrac{{{b^2}}}{{4{a^2}}} - \dfrac{{{b^2}}}{{4{a^2}}} + \dfrac{c}{a}} \right]\\ \Rightarrow \dfrac{1}{a}y = \left[ {{{\left( {x + \dfrac{b}{{2a}}} \right)}^2} - \dfrac{{{b^2} - 4ac}}{{4{a^2}}}} \right]\\ \Rightarrow \dfrac{1}{a}y = {\left( {x + \dfrac{b}{{2a}}} \right)^2} - \dfrac{\Delta }{{4{a^2}}}\\ \Rightarrow \dfrac{1}{a}\left( {y + \dfrac{\Delta }{{4a}}} \right) = {\left( {x + \dfrac{b}{{2a}}} \right)^2} \end{array}\] elde edilir. Böylece merkezi \[M\left( { - \dfrac{b}{{2a}}, - \dfrac{\Delta }{{4a}}} \right)\] ve parametresi \[p = \dfrac{1}{{2a}}\] olan ötelenmiş parabol denklemi elde ederiz. Öteleme vektörü \[\overrightarrow u = \left( {-\dfrac{b}{{2a}},-\dfrac{\Delta }{{4a}}} \right)\] olduğundan parabolün doğrultmanı \[\begin{array}{l}
y = - \dfrac{p}{2} - \dfrac{\Delta }{{4a}}\\ \Rightarrow y = - \dfrac{1}{{4a}} - \dfrac{\Delta }{{4a}} = - \dfrac{{\Delta + 1}}{{4a}} \end{array}\] olur. Demek ki parabolün dik kesişen teğetlerinin kesim noktalarının geometrik yeri aynı zamanda parabolün doğrultmanıdır.
Soru
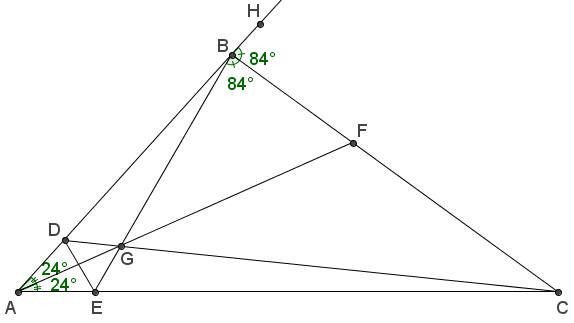
Şekildeki \(ABC\) üçgeninde, \([CD] \cap [BE] \cap [AF] = \left\{ G \right\}\), \(m(\widehat {BAF}) = m(\widehat {CAF}) = {24^ \circ }\), \(m(\widehat {CBE}) = m(\widehat {CBH}) = {84^ \circ }\) ve \(A\), \(B\) , \(H\) doğrusal olduğuna göre, \[m(\widehat {CDE})\] kaç derecedir?
Çözüm 1 - Temel GÖKÇE
\(\triangle EAB\) ninde \([BC]\) dış açıortay olduğundan \(\dfrac{{|CE|}}{{|CA|}} = \dfrac{{|BE|}}{{|BA|}}\) dır.
Buradan \[|CE| = \frac{{|CA|.|BE|}}{{|BA|}}\] elde edilir. \(\triangle ABC\) ninde \([AF]\) iç açıortay olduğundan \(\dfrac{{|CA|}}{{|AB|}} = \dfrac{{|CF|}}{{|BF|}}\) dir.
Buradan \[|BF| = \frac{{|AB|.|CF|}}{{|CA|}}\] olur.
\(\triangle ABC\) ninde Seva teoremi uygulanırsa \[\frac{{|CE|}}{{|EA|}}.\frac{{|AD|}}{{|DB|}}.\frac{{|BF|}}{{|FC|}} = 1\] olur. Yukarıda bulduğumuz eşitlikleri yerine yazarsak \[\frac{{|CA|.|BE|}}{{|BA|.|EA|}}.\frac{{|AD|}}{{|DB|}}.\frac{{|AB|.|CF|}}{{|FC|.|CA|}} = 1\] olur. Sadeleştirmeler yapılırsa \[\frac{{|BE|}}{{|EA|}} = \frac{{|DB|}}{{|AD|}}\] elde edilir. O halde \([ED]\), \(\triangle AEB\) nin iç açıortayıdır. Bu durumda \(m(\widehat {AEG}) = {120^ \circ }\) olduğundan \[m(\widehat {AED}) = m(\widehat {DEB}) = m(\widehat {BEC}) = {60^ \circ }\] olur.
Demek ki \([EB]\) de \(\triangle ADE\) nin dış açıortayıdır. Bu üçgende \([AF]\) de iç açıortay olduğundan \([DC]\) de dış açıortay olur. Böylece \[m(\widehat {CDE}) = {54^ \circ }\] bulunur.
Çözüm 2 - Süleyman SÖYLER
Süleyman hocam, \(m(\widehat {AFB}) = {60^ \circ }\) olduğu sürece geçerli olan bir genelleme üretti. Resmi daha iyi görmek için sağ tıklayıp farklı kaydet diyerek bilgisayarınıza yükleyip açabilirsiniz.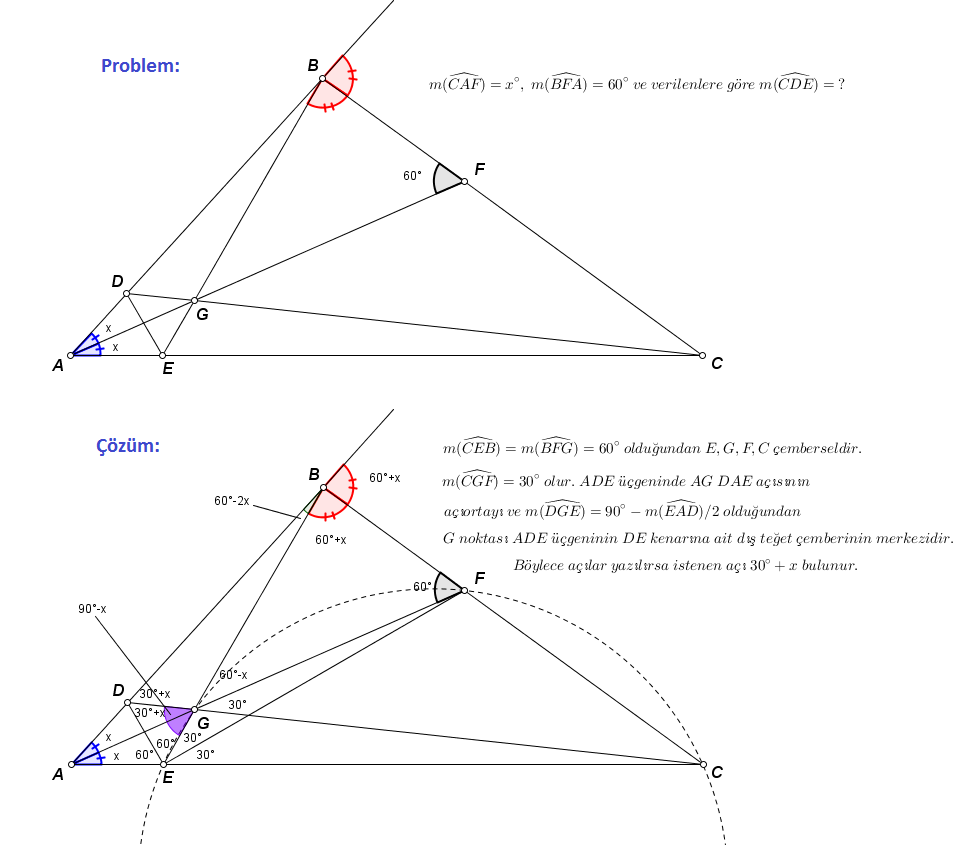

Çözümler için Temel GÖKÇE ve Süleyman SÖYLER öğretmenlerime teşekkür ediyorum.
Sorunun özünde \(\triangle AEB\) nin \(A\) ve \(E\) köşelerinden çıkan iç açıortaylarının sırasıyla kenarları kestiği noktalar olan \(G\) ve \(D\) ile, \(B\) köşesinden çıkan dış açıortayının \(AE\) yi kestiği nokta olan \(C\) nin daima doğrusal olması yatıyor. Bunun ispatı, 1. çözümde geçen yöntemle yapılabilir.
Soru
\(A = \{ 1,2,3,...,n\} \) kümesi verilsin.
- \(A\) kümesinin boş kümeden farklı herhangi bir alt kümesi \(A_i\) olsun. \(A_i\) kümesinin elemanlarının çarpımı da \(X_i\) olsun. Buna göre, tüm \(X_i\) değerlerinin toplamını \(n\) cinsinden ifade ediniz.
- \(A\) kümesinin boş kümeden farklı ve eleman sayısı çift olan herhangi bir alt kümesi \(B_i\) olsun. Bu kümenin elemanlarının çarpımı da \(Y_i\) olsun. Buna göre, tüm \(Y_i\) değerlerinin toplamını \(n\) cinsinden ifade ediniz.
- \(A\) kümesinin boş kümeden farklı ve eleman sayısı tek olan herhangi bir alt kümesi \(C_i\) olsun. Bu kümenin elemanlarının çarpımı da \(Z_i\) olsun. Buna göre, tüm \(Z_i\) değerlerinin toplamını \(n\) cinsinden ifade ediniz
Çözüm
Öncelikle ilk ifadenin çözümünü verelim. Bunun için \[f(x) = (x - 1)(x - 2)(x - 3)...(x - n)\] fonksiyonunu düşünelim. Bu fonksiyonun kökleri \(A = \{ 1,2,3,...,n\} \) kümesini oluşturmaktadır. Fonksiyonu \[f(x) = {x^n} + {b_1}{x^{n - 1}} + {b_2}{x^{n - 2}} + ... + {b_{n - 1}}x + {b_n}\] biçiminde yazarsak kökler toplamının \( - {b_1}\), köklerin ikişerli çarpımlarının toplamının \({b_2}\), köklerin üçerli çarpımlarının toplamının \(-b_3\) ..., köklerin tamamının çarpımının \(n\) nin çift veya tek oluşuna göre \( \pm {b_n}\) olduğunu Vieta formüyle görebiliriz. O halde \(n\) nin çift ve tek oluşuna göre durumu açıklayalım.
\(n\) çift ise \[\begin{array}{l} f( - 1) = ( - 2)( - 3) ... ( - 1 - n) = 1 - {b_1} + {b_2} - {b_3} + ... + {b_n}\\ \Rightarrow - {b_1} + {b_2} - {b_3} + ... + {b_n} = (n + 1)! - 1 \end{array}\] olurken
\(n\) tek ise \[\begin{array}{l} f( - 1) = ( - 2)( - 3) ... ( - 1 - n) = - 1 + {b_1} - {b_2} + {b_3} - ... - {b_n}\\ \Rightarrow - {b_1} + {b_2} - {b_3} + ... + {b_n} = (n + 1)! - 1 \end{array}\] olmaktadır. (İkinci durumda \(n\) tek olduğundan \(( - 2)( - 3) ... ( - 1 - n) = - (n + 1)!\) olduğuna dikkat ediniz.)
O halde her iki durumda da köklerin birbirleriyle farklı çarpımları toplamının \((n+1)!-1\) olduğunu görüyoruz. Bu, \(A = \{ 1,2,3,...,n\} \) kümesi için ilk soruda aradığımız cevaptan başka birşey değildir. Çünkü \(A\) kümesinin belli bir sayıda eleman (örneğin 2 eleman) ieçeren alt kümelerin elemanlarının çarpımları toplamı ile yazdığımız \(f\) fonksiyonun köklerinin belli bir miktarda (örneğin ikişerli biçimde) çarpımının toplamı aynıdır. O halde ilk soru için cevabımız \[(n + 1)! - 1\] dir.
Şimdi ikinci sorunun çözümünü verelim. Dikkat ederseniz yazdığımız \(f\) fonksiyonu için \(f(1) = 0\) dır. Öte yandan \[f(1) = 1 + {b_1} + {b_2} + ... + {b_n}\] dir. Ayrıca \(n\) çift için \[f( - 1) = 1 - {b_1} + {b_2} - {b_3} + ... + {b_n}=(n+1)!\] olduğunu yukarıda ifade etmiştik. \(f(1)\) ve \(f(-1)\) değerlerini toplarsak \[2(1 + {b_2} + {b_4} + ... + {b_n}) = (n + 1)!\] bulunur. Demek ki \[{b_2} + {b_4} + ... + {b_n} = \frac{{(n + 1)!}}{2} - 1\] dir. (\(n\) tek için de aynı durumun geçerli olacağını siz gösteriniz.) O halde \(A\) kümesinin boş kümeden farklı çift sayıda eleman içeren kümelerindeki elemanların çarpımları toplamı \[\frac{{(n + 1)!}}{2} - 1\] olur.
Son sorumuzada \(f(1)\) ve \(f(-1)\) farkından cevap verebiliriz, ama en kısa çözümümüz tabiki tüm durumdan çift olanların durumunu çıkarmak olacaktır. Yani \(A\) kümesinin boş kümeden farklı tek sayıda eleman içeren kümelerindeki elemanların çarpımları toplamı \[(n + 1)! - 1 - \left( {\frac{{(n + 1)!}}{2} - 1} \right) = \frac{{(n + 1)!}}{2}\] bulunur.
Soru
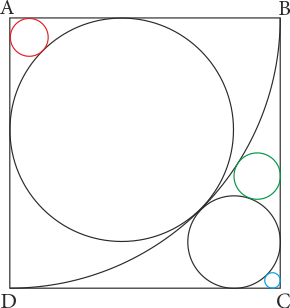 Şekildeki \(ABCD\) karesinde \(A\) merkezli çeyrek çember ile 5 çember verilmiştir. Çemberler şekildeki gibi kareye ve birbirine teğettir. Mavi ve kırmızı çemberlerlerin yarıçapları toplamı \(\sqrt 2 \) olduğuna göre, yeşil çemberin yarıçapı kaç birimdir?
Şekildeki \(ABCD\) karesinde \(A\) merkezli çeyrek çember ile 5 çember verilmiştir. Çemberler şekildeki gibi kareye ve birbirine teğettir. Mavi ve kırmızı çemberlerlerin yarıçapları toplamı \(\sqrt 2 \) olduğuna göre, yeşil çemberin yarıçapı kaç birimdir?
Çözüm
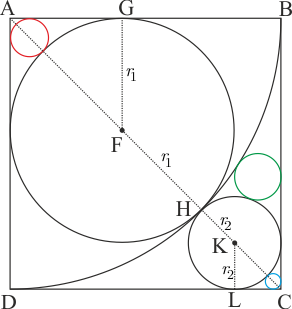
\(AGF\) üçgeninde \(|AF| = {r_1}\sqrt 2\) dir. \(KLC\) üçgeninde \(|KC|={r_2}\sqrt 2\) dir. Bu durumda \(|AC| = \left( {{r_1} + {r_2}} \right)\left( {\sqrt 2 + 1} \right)\) olur. \(|AH| = {r_1}\left( {\sqrt 2 + 1} \right)\) karenin bir kenarına eşit olduğundan \(|AC| = \sqrt 2 |AH|\) olur. O halde \(\left( {{r_1} + {r_2}} \right)\left( {\sqrt 2 + 1} \right) = \sqrt 2 {r_1}\left( {\sqrt 2 + 1} \right)\) eşitliğinden $$\dfrac{r_2}{r_1} = \sqrt{2} -1 \qquad (...1)$$ bulunur.
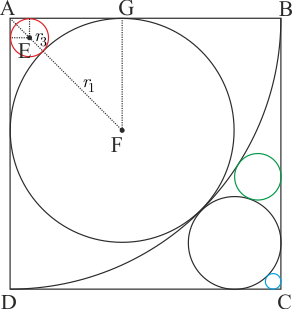
Şekildeki gibi kırmızı çemberin yarıçapına \(r_3\) dersek ve merkeziyle karenin kenarlarına dik çizip gerekli işlemleri yaparsak \(AF| = |AE| + |EF| = {r_3}\sqrt 2 + {r_3} + {r_1}\) olurken \(AGF\) üçgeninde \(|AF| = {r_1}\sqrt 2 \) olduğundan \({r_3}\sqrt 2 + {r_3} + {r_1} = {r_1}\sqrt 2 \) olur. Bu eşitlikten \[r_3=r_1.\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\qquad(...2)\] elde edilir. Benzer biçimde mavi çemberin yarıçapına \(r_4\) dersek, ilk şekilde \(|KC| = {r_2} + {r_4} + {r_4}\sqrt 2 \) bulunur. Ayrıca \(|KC| = {r_2}\sqrt 2 \) olduğundan \[r_4=r_2.\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\qquad(...3)\] elde edilir. Elde ettiğimiz son iki eşitliği taraf tarafa oranlarsak \(\dfrac{{{r_4}}}{{{r_3}}} = \dfrac{{{r_2}}}{{{r_1}}} = \sqrt {2} - 1\) bulunur. Soruda \({r_3} + {r_4} = \sqrt 2 \) verildiğinden ve \({r_4} = {r_3} \cdot \left( {\sqrt {2} - 1} \right)\) olduğundan \[r_3=1 \qquad r_4=\sqrt{2}-1\] bulunur. Bu değerleri (...2) ve (...3) te yerine yazarsak \[r_1=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}\qquad r_2=\sqrt{2}+1\] bulunur.
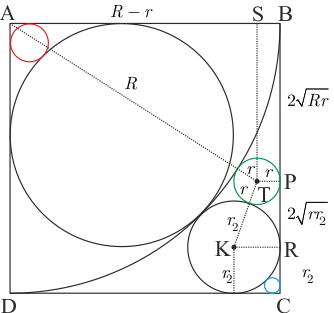
Şekildeki gibi çeyrek çemberin yarıçapına \(R\) ve yeşil çemberin yarıçapına \(r\) diyelim. \(|AT|=R+r\) ve \(|AS|=R-r\) olacağından \(|ST|=|BP|=2\sqrt{Rr}\) bulunur. Benzer mantık \(KTPR\) dik yamuğunda yapılırsa \(|PR|=2\sqrt{rr_2}\) bulunur. \(|RC|=r_2\) olduğundan, karenin bir kenarı \(|BC| = {r_2} + 2\sqrt r \left( {\sqrt {{r_2}} + \sqrt R } \right)\) bulunur. Ayrıca karenin bir kenarı \(R\) olduğundan \(R = {r_2} + 2\sqrt r \left( {\sqrt {{r_2}} + \sqrt R } \right)\) olur. Bu denklemden \[2\sqrt r = \frac{{R - {r_2}}}{{\sqrt R + \sqrt {{r_2}} }} \Rightarrow 2\sqrt r = \sqrt R - \sqrt {{r_2}} \qquad (...4)\] elde edilir. Bu eşitliğin karesini alırsak \[4r = R + {r_2} - 2\sqrt {R{r_2}}\qquad(...5)\] olur. İlk şekilden görüleceği üzere \(|AH| = R = {r_1}\left( {\sqrt 2 + 1} \right)\) ve (...1) nolu eşitlikten \({r_2} = {r_1} \cdot \left( {\sqrt 2 - 1} \right)\) değerleri (...5) te yerine yazılırsa \[4r = {r_1}\left( {\sqrt 2 + 1} \right) + {r_1}\left( {\sqrt 2 - 1} \right) - 2\sqrt {{r_1}\left( {\sqrt 2 + 1} \right) \cdot {r_1}\left( {\sqrt 2 - 1} \right)} \] \[ \Rightarrow r = {r_1} \cdot \frac{{\sqrt 2 - 1}}{2}\qquad(...6)\] bulunur. Bulduğumuz \({r_1} = \dfrac{{\sqrt 2 + 1}}{{\sqrt 2 - 1}}\) değerini yerine yazarsak \[r = \dfrac{{\sqrt 2 + 1}}{2}\] bulunur.
Sonuç olarak çemberlerden herhangi birinin yarıçapı ile diğer çemberlerin yarıçaplarını ifade edebilecek genellikte bir çözüm sunmuş olduk.
Soru
\(x \in R\) için \(x\sqrt x - 2\sqrt x = 1\) olduğuna göre, \[{x^2} - 3x\] ifadesinin değeri kaçtır?
Çözüm
\(x\sqrt x - 2\sqrt x - 1 = 0\) biçimine getirelim ve \(2\sqrt x\) yerine \(\sqrt x + \sqrt x \) yazalım. \[x\sqrt x - \sqrt x - \sqrt x - 1 = 0\] \[\sqrt x (x - 1) - \sqrt x - 1 = 0\]\[\sqrt x (\sqrt x - 1)(\sqrt x + 1) - (\sqrt x + 1) = 0\]\[(\sqrt x + 1)\left[ {\sqrt x .(\sqrt x - 1) - 1} \right] = 0\]\[(\sqrt x + 1)\left[ {x - \sqrt x - 1} \right] = 0\] olur. Bu durumda \(\sqrt x = - 1\) veya \(x - \sqrt x - 1 = 0\) dır. Fakat \(\sqrt x = - 1\) olamayacağından \(x - \sqrt x - 1 = 0\) olur. \(\sqrt{x}\) i eşitliğin diğer tarafına alırsak \[x - 1 = \sqrt x \] olur. Bu eşitliğin her iki tarafının da karesini alırsak \[\begin{array}{l}{x^2} - 2x + 1 = x\\ \Rightarrow {x^2} - 3x = - 1\end{array}\] bulunur.
Soru
Bir doğru parçası eş zamanlı olarak 4 parçaya ayrılıyor. Bu parçaların bir dışbükey dörtgen belirtme olasılığı kaçtır?
Çözüm
Sorunun çözümüne geçmeden önce "aynı anda 3 parçaya bölünen doğru parçasının bu parçalarının üçgen belirtme, dar açılı üçgen belirtme ve geniş açılı üçgen belirtme olasığı" üzerine eski çalışmamı izlemenizi tavsiye ederim.
Öncelikle şunu kanıtlayalım:
"Düzgün dörtyüzlü için alınan bir P noktasından yüzeylerine çizilen dikmelerin uzunlukları toplamı dörtyüzlünün yüksekliğine eşittir."
Kanıt:
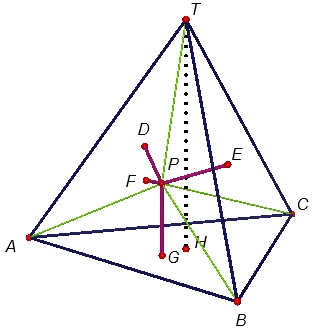
Şekildeki gibi \((T,ABC)\) düzgün dörtyüzlüsü içinde bir P noktası alınsın ve sırasıyla yüzeylerine çizilen dikmeleri \([PD]\), \([PE]\), \([PF]\) ve \([PG]\) olsun. Dörtyüzlünün yüksekliği \([TH]\) ve \([PA]\), \([PB]\), \([PC]\), \([PT]\) çizilsin. Bu durumda düzgün dörtyüzlüyü oluşturan \((P,ATB)\), \((P,ATC)\), \((P,BTC)\) ve \((P,ABC)\) piramitleri elde edilmiş olur. Bu piramitlerin taban alanları, dörtyüzlünün yüzeyleri olduğundan, eşittirler. Dörtyüzlünün bir yüzeyinin alanına \(S\) dersek, piramitlerin hacimleri sırasıyla \(\dfrac{1}{3} \cdot S \cdot |PF|\), \(\dfrac{1}{3} \cdot S \cdot |PD|\), \(\dfrac{1}{3} \cdot S \cdot |PE|\) ve \(\dfrac{1}{3} \cdot S \cdot |PG|\) dir. O halde bunların toplamı dörtyüzlünün hacmine eşit olmalıdır: \[\begin{array}{l}
\frac{1}{3} \cdot S \cdot |TH| = \frac{1}{3} \cdot S \cdot \left[ {|PF| + |PD| + |PE| + |PG|} \right]\\
\\
\Rightarrow |TH| = |PF| + |PD| + |PE| + |PG|
\end{array}\] olur.
Videoyu izleyerek görsel destek alabilirsiniz.
Video burada görüntülenecektir.
Bu kanıttan sonra belki tahmin etmişsinizdir; soruda verilen doğru parçası dörtyüzlünün yüksekliği \([TH]\) ve ayrılan dört parça \([PD]\), \([PE]\), \([PF]\) ve \([PG]\) olacak biçimde soruyu çözeceğiz. Parçaların dörtgen oluşturabilmesi için her birinin uzunluğu \([TH]\) ın yarısından küçük olmalıdır. Aksi halde dörtgen oluşmayacağı aşikardır. Bu şartın sağlanması için \(P\) noktasının
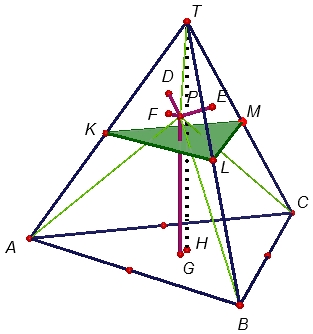
şekildeki gibi, taban köşeleri \((T,ABC)\) nin yan ayrıtlarının orta noktaları olan, \((T,KLM)\) düzgün dörtyüzlüsü içinde yer almaması gerekir. Çünkü bu durumda \[|PG| > \dfrac{{|TH|}}{2}\] olacaktır. Benzer biçimde \(P\) nin bulunmaması gereken bölgeler aşağıdaki şekilde verilmiştir.
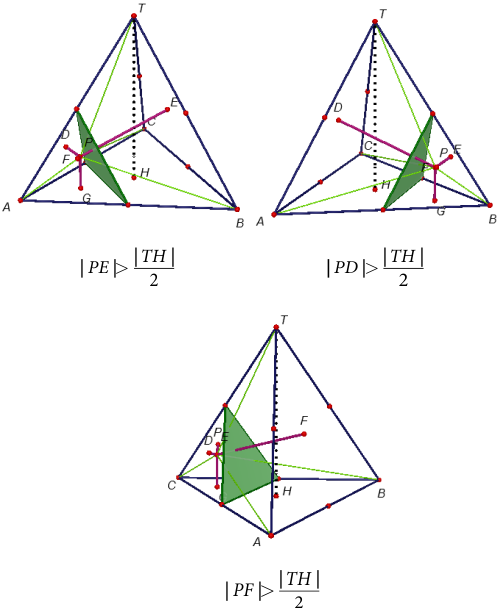
Benzerlik gereği düzgün dörtyüzlünün hacminin bunlardan birinin hacmine oranı \[{\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}\] dir. O halde \[{V_{(T,ABC)}} = 8V\] dersek; istenmeyen bölgenin hacmi \[{V_{istenmeyen}} = 4V\] olacaktır. Böylece istenilen olasılık \[P = 1 - \frac{{4V}}{{8V}} = \frac{1}{2}\] bulunur.
Videoda \(P\) noktasının bulunması gereken bölgenin asında düzgün dörtyüzlünün orta sekizyüzlüsü olduğunu görebilirsiniz.
Video burada görüntülenecektir.
Esasında bu soruyu 5 parça için sorsaydık, her ne kadar 4.boyuta geçiyor olsak ve bunu çizemesekte, istenmeyen (hiper)bölge sayısının 5 ve benzerlik oranının \({\left( {\dfrac{1}{2}} \right)^4} = \dfrac{1}{{16}}\) olacağını sezebiliriz. Yani 5 gen oluşturma olasılığı \[P = 1 - \frac{{5V}}{{16V}} = \frac{{11}}{{16}}\] olurdu.
Genel olarak eş zamanlı olarak n parçaya bölünen bir doğru parçasının, bu parçalarının bir n-gen belirtme olasılığı \[1 - \frac{n}{{{2^{n - 1}}}}\] dir.
Bu konuyla ilgili değerli meslektaşım Lokman GÖKÇE'nin hazırladığı "Geometrik Olasılık" başlığı Geomania sitesinde ziyaret edilebilir.
Soru
\[{d_1}:2x = y = z\] \[{d_2}:x = 2y = z\] doğrularına teğet, yarıçapı \(\dfrac{3\sqrt{5}}{2}\) birim olan ve merkezi \(x-2y=0\) düzleminde bulunan kürelerin denklemlerini bulunuz.
Çözüm
Öncelikle \({d_1}\) doğrusunun doğrultu vektörünün \(\overrightarrow {{u_1}} = (1,2,2)\) ve \({d_2}\) doğrusunun doğrultu vektörünün \(\overrightarrow {{u_2}} = (2,1,2)\) olduğunu görelim. Ayrıca doğruların \(O(0,0,0)\) noktasında kesiştiğini görelim. İstenilen kürelerin merkezi \(x = 2y\) düzleminde olduğundan bu noktaları \(P(2y,y,z)\) biçiminde gösterebiliriz. Küreler doğrulara teğet olduğundan, merkezin doğrulara olan uzaklıkları eşit ve yarıçap kadar olmalıdır. (Noktanın doğruya uzaklığı için tıklayınız!) Yani \[\frac{{||\overrightarrow {OP} \times \overrightarrow {{u_1}} |{\kern 1pt} |}}{{||\overrightarrow {{u_1}} ||}} = \frac{{||\overrightarrow {OP} \times \overrightarrow {{u_2}} |{\kern 1pt} |}}{{||\overrightarrow {{u_2}} ||}} = \frac{3\sqrt 5}{2} \] olmalıdır. Bu eşitlikte \(||\overrightarrow {{u_1}} || = ||\overrightarrow {{u_2}} || = 3\) olduğuna dikkat edersek \[||\overrightarrow {OP} \times \overrightarrow {{u_1}} |{\kern 1pt} | = ||\overrightarrow {OP} \times \overrightarrow {{u_2}} |{\kern 1pt} |\] eşitliğini çözmeye çalışalım. \[\overrightarrow {OP} \times \overrightarrow {{u_1}} = \left| {\begin{array}{*{20}{c}}
{\overrightarrow {{e_1}} }&{\overrightarrow {{e_2}} }&{\overrightarrow {{e_3}} }\\
{2y}&y&z\\
1&2&2
\end{array}} \right| = (2y - 2z\,,\,z - 4y\,,\,3y)\] ve \[\overrightarrow {OP} \times \overrightarrow {{u_2}} = \left| {\begin{array}{*{20}{c}}
{\overrightarrow {{e_1}} }&{\overrightarrow {{e_2}} }&{\overrightarrow {{e_3}} }\\
{2y}&y&z\\
2&1&2
\end{array}} \right| = (2y - z\,,\,2z - 4y\,,\,0)\] olur. Uzunluklarını eşitlersek \[y \cdot (9y + 4z) = 0\] denklemi elde edilir. Böylece \(y = 0\) için kürelerden birinin merkezi \[P(0,0,z)\] \(9y = -4z\) için ise bir \(k\) parametresine bağlı olarak diğer kürenin merkezi \[P(8k,4k,-9k)\] olacaktır. \(P(0,0,z)\) için \[\overrightarrow {OP} \times \overrightarrow {{u_1}} = ( - 2z,z,0)\] olacağından \[\frac{{||\overrightarrow {OP} \times \overrightarrow {{u_1}} ||}}{{||\overrightarrow {{u_1}} ||}} = \frac{{3\sqrt 5 }}{2}\] eşitliğinde yerine yazarsak \(|z|=\dfrac{9}{2}\) olur. Böylece bu şartlarda merkezleri sırasıyla \[P\left( {0\,,0\,,\,\frac{9}{2}} \right)\] ve \[P\left( {0\,,0\,,\,-\frac{9}{2}} \right)\] olan iki küre elde edilir. Bu kürelerin denklemleri \[{x^2} + {y^2} + {\left( {z - \frac{9}{2}} \right)^2} = \frac{{45}}{4}\] ve \[{x^2} + {y^2} + {\left( {z + \frac{9}{2}} \right)^2} = \frac{{45}}{4}\] olacaktır. Öte yandan \(P(8k,4k,-9k)\) için \[\overrightarrow {OP} \times \overrightarrow {{u_1}} = (26k\,, - 25k\,,\,12k)\] olacağından \[\frac{{||\overrightarrow {OP} \times \overrightarrow {{u_1}} ||}}{{||\overrightarrow {{u_1}} ||}} = \frac{{3\sqrt 5 }}{2}\] eşitliğinde yerine yazılırsa \[|k| = \frac{9}{{34}}\] bulunur. Böylece tekrar iki farklı merkez elde ederiz: \[P\left( {\frac{{36}}{{17}}\,,\,\frac{{18}}{{17}}\,,\,\frac{{-81}}{{34}}} \right)\] ve \[P\left( {-\frac{{36}}{{17}}\,,\,-\frac{{18}}{{17}}\,,\,\frac{{81}}{{34}}} \right)\] bulunur. Kürelerin denklemleri de \[{\left( {x - \frac{{36}}{{17}}} \right)^2} + {\left( {y - \frac{{18}}{{17}}} \right)^2} + {\left( {z + \frac{{81}}{{34}}} \right)^2} = \frac{{45}}{4}\] ve \[{\left( {x + \frac{{36}}{{17}}} \right)^2} + {\left( {y + \frac{{18}}{{17}}} \right)^2} + {\left( {z - \frac{{81}}{{34}}} \right)^2} = \frac{{45}}{4}\] olur. Özetle verilen şartlara uygun 4 farklı küre vardır.
Soru
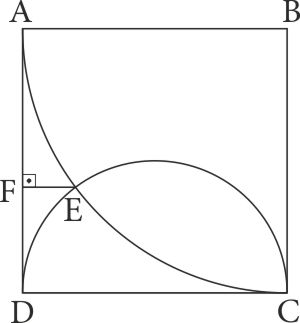
Şekilde \(B\) merkezli çeyrek çember \(ABCD\) karesine içten \(A\) ve \(C\) noktalarında; \([DC]\) çaplı yarım çember ise \(D\) ve \(C\) noktalarında teğettir. \(E\) noktası kesim noktasıdır. \([EF] \bot [AD]\) ve \(|EF|=2\) birim olduğuna göre, \(ABCD\) karesinin alanı kaç birim karedir?
Çözüm 1
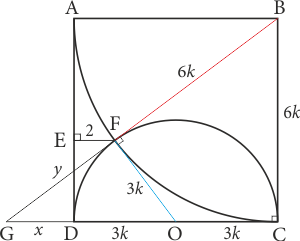
Şekildeki gibi \(BF \cap CD = \{ G\} \) olacak biçimde \([BG]\) ve \([CG]\) çizilsin. \(O\) merkezli yarım çember için \([OF]\) çizilsin. \(|OF|=|OC|=|OD|=3k\) olsun. \(B\) merkezli çeyrek çember için \(|BC|=|BF|=6k\) olur. \([BC]\), \(B\) noktasından \(O\) merkezli yarım çembere çizilen teğet ve \(|BF|=|BC|\) olduğundan \([BF]\) de \(O\) merkezli yarım çembere \(E\) de teğettir. Ek olarak \(OCBF\) dörtgeninin bir deltoid olduğu da görülebilirdi. \([OF]\perp[BG]\) gereği \(BGC \sim OGF\) olur. \(|GD|=x\) ve \(|GF|=y\) dersek benzerlik gereği \[\frac{3k}{{6k}} = \frac{y}{{x + 6k}} = \frac{{x + 3k}}{{y + 6k}}\] olur. Bu eşitlikten \(x = 2k\) ve \(y=4k\) bulunur. Demek ki \(FGO\) ve \(BCG\) üçgenleri birer 3-4-5 üçgenleriymiş.
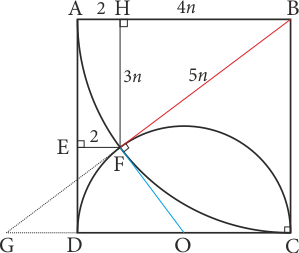
Şekildeki gibi \([FH]\perp[AB]\) çizilirse \(OFG\sim FHB\) olacağından \(FHB\) üçgeni de bir 3-4-5 üçgenidir. \(|HF|=3n\), \(|HB|=4n\) ve \(|BF|=5n\) dersek ve \(|BF|=|BA|\) eşitliği görülürse \[4n+2=5n\] olacağından \(n=2\) ve karenin bir kenar uzunluğu \(10\) birim bulunur. Böylece \[Alan(ABCD)=100\,br^2\] olur.
Çözüm 2 (Erhan Erdoğan)

Soru
Uzayda \(d_1:2x + z = 4;\; y = 0\) ve \(d_2:y + 2z = 4;\; x = 0\) doğrularının her ikisiyle de dik kesişen doğrunun denklemini bulunuz.
Çözüm
Çözümde geçen detayları anlamak için "Aykırı Doğrular" içeriğini inceleyiniz.
Öncelikle \(d_1\) doğrusunun doğrultu vektörü \(\overrightarrow {{u_1}} = ( - 1,0,2)\) ve sabit noktası \(A(0,0,4)\); \(d_2\) doğrusunun ise doğrultu vektörü \(\overrightarrow {{u_2}} = ( 0,-2,1)\) ve sabit noktası \(A(0,0,2)\) alınabilir. Böylece \(\overrightarrow {AB} = (0,0, - 2)\) olur. Bu üç vektörün belirteceği determinant hesaplanırsa \(0\) dan farklı olduğu görülecektir. Yani bu doğrular aykırı doğrulardır. Bu durumda her ikisiyle kesişen ve her ikisine de dik olan doğru, bu doğruların birbirine en yakın noktalarından geçen doğrudur. \(\overrightarrow N = \overrightarrow {{u_1}} \times \overrightarrow {{u_2}} = (4,1,2)\) vektörünü ve \(\overrightarrow N \times \overrightarrow {{u_2}} = (5, - 4, - 8)\) vektörünü kullanarak \(d_1\) doğrusunun \(d_2\) doğrusuna en yakın noktası \(C = A + k\overrightarrow {{u_1}} \) bulalım. \[ < \overrightarrow {AB} - k\overrightarrow {{u_1}}\quad ,\quad \overrightarrow N \times \overrightarrow {{u_2}} > = 0\] olacağından ifadeler yerine yazılırsa \[k = - \dfrac{{16}}{{21}}\] bulunur. Böylece \[C\left( {\dfrac{{16}}{{21}},0,\dfrac{{52}}{{21}}} \right)\] olur. Ayrıca dikkat edilirse \(\overrightarrow N \) aradığımız doğrunun doğrultu vektörü olacaktır. O halde istenilen doğrunun denklemi gerekli düzenlemelerle : \[\dfrac{{x - 16/21}}{4} = y = \dfrac{{z - 52/21}}{2}\] olarak ifade edilebilir.
Soru 1
\(A= \left \{ 1,2,3,4,5,6,7,8,9 \right \}\) kümesinin alt kümelerinin eleman sayılarının toplamı kaçtır?
\(A= \left \{ 1,2,3,...,n \right \}\) kümesinin alt kümelerinin eleman sayılarının toplamını veren bir formül elde ediniz.
Çözüm
Öncelikle şu soruya cevap arayalım: \(A\) kümesinin herhangi bir elemanı kaç alt kümede bulunur? Örneğin \(A\) kümesinin kaç alt kümesinde "\(1\)" eleman olarak bulunur? Bunun cevabı basit, tabii ki \(2^8\) farklı alt kümede "\(1\)" eleman olarak bulunur. Yani "\(1\)" elemanı, alt kümelerin eleman sayılarının toplamı hesaplanırken, \(2^8\) defa sayılacaktır. Aynı durum diğer elemanlar için de geçerlidir. Her bir eleman \(2^8\) farklı alt kümenin bir elemanı olacak ve alt kümelerin eleman sayılarının toplamı hesaplanırken her biri \(2^8\) defa sayılacaktır. O halde cevabımız \(9.2^8\) dir.
Demek ki \(n\) elemanlı bir kümenin tüm alt kümelerinin eleman sayılarının toplamı \(n.2^{n-1}\) dir.
Aslında bu cevabımızla bir özdeşlik elde etmiş oluyoruz:$$1\binom{n}{1}+2\binom{n}{2}+3\binom{n}{3}+...+n\binom{n}{n}=n.2^{n-1}$$ dir.
Soru 2
\(A= \left \{ 1,2,3,4,5,6,7,8,9 \right \}\) kümesinin alt kümelerindeki sayıların toplamı kaçtır?
\(A= \left \{ 1,2,3,...,n \right \}\) kümesinin alt kümelerindeki sayıların toplamını veren bir formül elde ediniz.
Çözüm
İlk sorudaki çözüm mantığımızla bu sorumuzun cevabı da \((1+2+3+...+9)2^{8}=45.2^8\) olur. Genel olarak \(A= \left \{ 1,2,3,...,n \right \}\) kümesinin alt kümelerindeki sayıların toplamı $$(1+2+3+...+n)2^{n-1}=n(n+1).2^{n-2}$$ olacaktır.
