Soru
\(n \geqslant 0\) doğal sayısı için \[{\left( {\begin{array}{*{20}{c}}n \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
2
\end{array}} \right)^2} + \cdot \cdot \cdot + {\left( {\begin{array}{*{20}{c}}
n \\
n
\end{array}} \right)^2} = \left( {\begin{array}{*{20}{c}}
{2n} \\
n
\end{array}} \right)\] eşitliğini kanıtlayınız.
Çözüm 1
En basit biçimiyle \(n\) tane erkek ve \(n\) tane kadın arasından \(n\) adet kişinin kaç farklı biçimde seçileceği sorusunun iki farklı çözümünün getirdiği bir eşitlik olarak düşünülebilir. Toplamda \(2n\) kişi olduğundan, bunlar arasından \(n\) kişi \[\left( {\begin{array}{*{20}{c}}
{2n}\\ n \end{array}} \right)\] farkı biçimde seçilebilir. Öte yandan bu seçimi erkek-bayan seçimleriyle yaparsak;
\(n\) kadın ve \(0\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right)^2}\)
\(n-1\) kadın ve \(1\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right)^2}\)
\(n-2\) kadın ve \(2\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ n-2 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right)^2}\)
.
.
.
\(1\) kadın ve \(n-1\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right)^2}\)
\(0\) kadın ve \(n\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right)^2}\)
olacağından toplamda \[{\left( {\begin{array}{*{20}{c}}
n \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
2
\end{array}} \right)^2} + \cdot \cdot \cdot + {\left( {\begin{array}{*{20}{c}}
n \\
n
\end{array}} \right)^2}\] olur. Böylece kanıt tamamlanır.
Çözüm 2
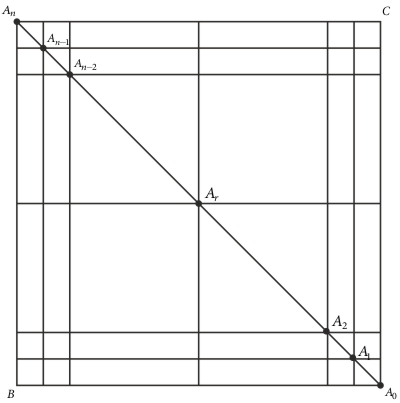
Şekildeki gibi birim karelerden oluşan \(n \times n\) ızgaranın \(B\) köşesinden \(C\) köşesine \(1\) birim sağa ve \(1\) birim yukarı hareket biçimleriyle çizilebilecek farklı yol sayısı \(n\) adet sağ ve \(n\) adet yukarı hareket olduğundan \[\left( {\begin{array}{*{20}{c}}
{2n}\\
n
\end{array}} \right)\] kadardır.
Öte yandan
\(A_0\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_0\) e olan yol sayısı ile \(A_0\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right)\);
\(A_1\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_1\) e olan yol sayısı ile \(A_1\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right)\);
\(A_2\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_2\) e olan yol sayısı ile \(A_2\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right)\);
.
.
\(A_r\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_r\) e olan yol sayısı ile \(A_r\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ r \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ r \end{array}} \right)\);
.
.
\(A_{n-2}\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_{n-2}\) e olan yol sayısı ile \(A_{n-2}\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ n-2 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n-2 \end{array}} \right)\);
\(A_{n-1}\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_{n-1}\) e olan yol sayısı ile \(A_{n-1}\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right)\);
\(A_{n}\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_{n}\) e olan yol sayısı ile \(A_{n}\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right)\);
olacağından bunların toplamı tüm yol sayısını verecektir. Böylece kanıt tamamlanır.
Çözüm 3
Bir diğer çözüm de \[ {(1 + x)^n} \cdot {(1 + x)^n} = {(1 + x)^{2n}}\] eşitliğinde her iki tarafta da \(x^n\) teriminin katsayısını bulunurak elde edilebilir. Eşitliğin sağında bunun \[\left( {\begin{array}{*{20}{c}}
{2n}\\
n
\end{array}} \right)\] olduğu açıktır. Sol tarafta ise birinci çarpandan gelecek olan \(x^r\) ile ikinci çarpandan gelecek olan \(x^{n-r}\) teriminin katsayıları çarpılacağından \(x^r.x^{n-r}=x^n\) nin katsayısı \[\left( {\begin{array}{*{20}{c}}
n\\
r
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
n\\
{n - r}
\end{array}} \right) = {\left( {\begin{array}{*{20}{c}}
n\\
r
\end{array}} \right)^2}\] olacaktır. \(r=0\) dan \(r=n\) ye kadar bu işlem yapılırsa istenilen eşitlik kanıtlanmış olur.

