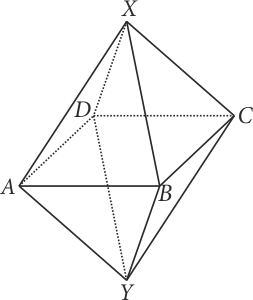
Şekildeki gibi bir sekizyüzlü düşünelim. Faremiz $X$ noktasına bırakılsın. Dolayısıyla $Y$ noktasına geldiğinde labirentten çıkmış olacaktır. Farenin $X$ noktasındayken labirentten ortalama çıkma (labirentten ortalama kurtulma) süresine $x$ diyelim. Benzer biçimde, fare $A$ noktasındayken labirentten ortalama çıkma süresine de $a$ diyelim. Dikkat edilirse, $B$, $C$ ve $D$ noktaları için de ortalama çıkma süresi $A$ noktası ile aynı yani $a$ olacaktır. Tekrar $X$ noktasına geri dönelim. Bu noktadan $\dfrac{1}{4}$ er ihtimalle $A$, $B$, $C$ ve $D$ noktalarına gidebilir. O halde, \[x = \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) = a + t\] dir. Eklenen $t$ süreleri $X$ den diğer noktalara geçmek için kullanılan ayrıtlardan kaynaklanmaktadır. Şimdi aynı mantıkta $A$ noktasını düşünelim.

• $\dfrac{1}{4}$ olasılıkla $B$ ye gidebilir. Ayrıtta geçen $t$ süre ve $B$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + t)$ olur.
• $\dfrac{1}{4}$ olasılıkla $D$ ye gidebilir. Ayrıtta geçen $t$ süre ve $D$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + t)$ olur.
• $\dfrac{1}{4}$ olasılıkla $X$ e gidebilir. Ayrıtta geçen $t$ süre ve $X$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + 2t)$ olur.
• $\dfrac{1}{4}$ olasılıkla $Y$ ye gidebilir. Ayrıtta geçen $t$ süre eklenince: $\dfrac{1}{4}(t)$ olur.

O halde, $A$ noktasından ortalama çıkma süresi \[a = \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + 2t} \right) + \frac{1}{4}t\] dir. Bu denklemden \[a = 5t\] bulunur. Böylece, \[x = a + t = 5t + t = 6t\] elde edilir.