Soru
Ege, Irmak ve Çınar aralarında anlaşıp bir alışveriş merkezinde saat 12:00 ile 13:00 arasında buluşacaklardır. İlk gelen, herhangi biri 10 dakika içinde gelmezse, alışveriş merkezini terkedecektir. Eğer 10 dakika içinde biri gelirse, ikisi birlikte üçüncü kişiyi en fazla 10 dakika bekleyecektir.
Buna göre, Ege, Irmak ve Çınar'ın buluşma olasılığını hesaplayınız.
Çözüm
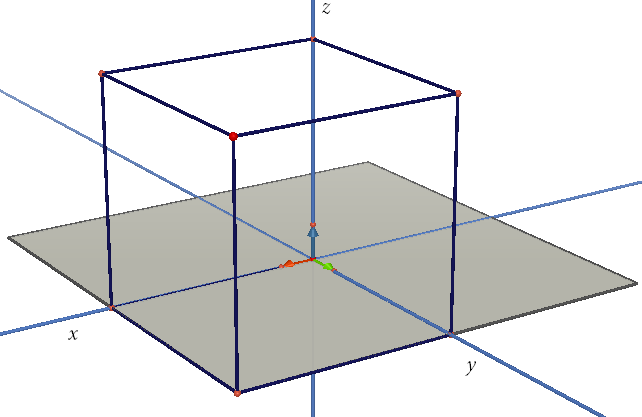
Öncelikle zaman dilimini bir reel aralığa indirgeyelim. 12:00 ı başlangıç ve 13:00 ı bitiş noktası seçerek [0,60] reel aralığını kullanacağız. Sırasıyla Ege, Irmak ve Çınar'ın gelme sürelerine \(x\), \(y\) ve \(z\) diyelim. Örneğin Çınar saat 12:32 de gelmişse \(z=32\) olacaktır. Böylece \((x,y,z)\) sıralı üçlüleri elde ederiz. Ayrıca \(0\le x \le 60\), \(0\le y \le 60\) ve \(0\le z \le 60\) olduğuna dikkat edin. Bu durumda bu sıralı \((x,y,z)\) üçlüleri aşağıdaki şekilde görüleceği üzere \(R^3\) te bir ayrıtı 60 birim olan bir küp belirteceklerdir. Böylece örnek uzayımız bu küpün hacmi olacaktır.
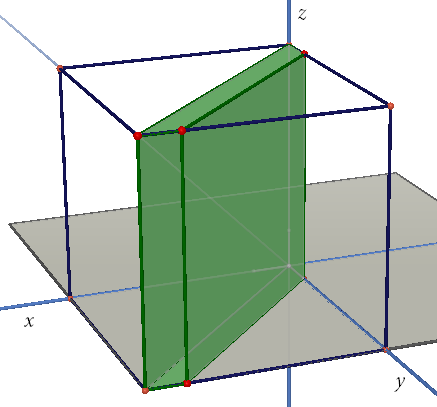
 Şimdi ilk gelenin Ege, sonra Irmak ve en son Çınar olduğunu varsayalım. Bu durumda buluşmanın gerçekleşebilmesi için Irmak'ın Ege'den sonra en çok 10 dakika içinde gelmiş olması gerekir. Yani \[x \le y \le x + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=x\) ve \(y=x+10\) düzlemleri arasında kalan bölge olacaktır.
Şimdi ilk gelenin Ege, sonra Irmak ve en son Çınar olduğunu varsayalım. Bu durumda buluşmanın gerçekleşebilmesi için Irmak'ın Ege'den sonra en çok 10 dakika içinde gelmiş olması gerekir. Yani \[x \le y \le x + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=x\) ve \(y=x+10\) düzlemleri arasında kalan bölge olacaktır.
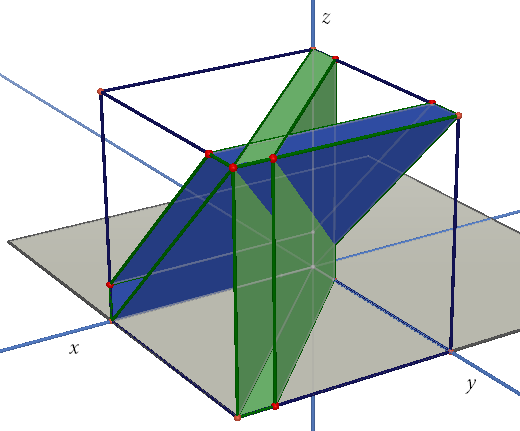
 Ayrıca Çınar'ında Irmak'tan en çok 10 dakika sonra gelmesi gerekeceğinden \[y \le z \le y + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=z\) ve \(z=y+10\) düzlemleri arasında kalan bölge olacaktır.
Ayrıca Çınar'ında Irmak'tan en çok 10 dakika sonra gelmesi gerekeceğinden \[y \le z \le y + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=z\) ve \(z=y+10\) düzlemleri arasında kalan bölge olacaktır.
 O halde buluşmanın bu şartlarda gerçekleşmesini gösteren bölge bu dört düzlemin ifade ettiği aşağıdaki videodaki gibi olacaktır.
O halde buluşmanın bu şartlarda gerçekleşmesini gösteren bölge bu dört düzlemin ifade ettiği aşağıdaki videodaki gibi olacaktır.
Oluşan bu cismin hacmini bulabilmek için cismi aşağıdaki videoda gösterildiği üzere \(y=10\) ve \(y=50\) düzlemleriye kesersek iki düzlem arasında kalan cisim kare eğik prizma olurken, uç noktalarda kalan parçalar kare eğik yarım prizmalar olacaktır.
Daha detaylı incelemek gerekirse, öncelikle aşağıdaki şekilde görülen yarım eğik kare prizmaya bakalım.
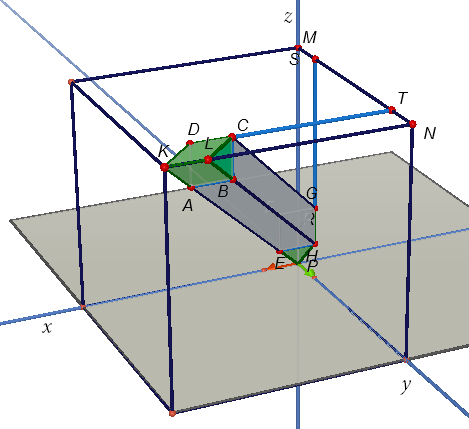 Prizmanın tabanı bir kenarı \(10\) birim olan \(ABCD\) karesidir. Yüksekliği ise \(|TN|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. Benzer biçimde aşağıdaki şekilde görüleceği üzere,diğer yarım eğik kare prizmanın
Prizmanın tabanı bir kenarı \(10\) birim olan \(ABCD\) karesidir. Yüksekliği ise \(|TN|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. Benzer biçimde aşağıdaki şekilde görüleceği üzere,diğer yarım eğik kare prizmanın
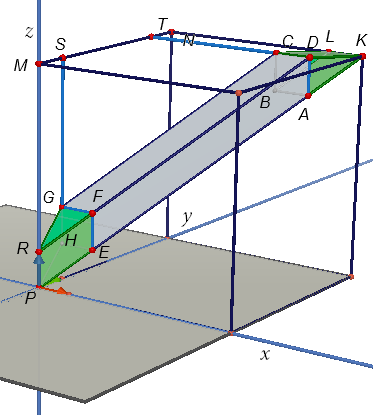 tabanı bir kenarı \(10\) birim olan \(GFEH\) karesidir. Yüksekliği ise \(|MS|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. O halde bu iki yarım prizmanın hacimleri toplamı \[{10^3}\] tür.
tabanı bir kenarı \(10\) birim olan \(GFEH\) karesidir. Yüksekliği ise \(|MS|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. O halde bu iki yarım prizmanın hacimleri toplamı \[{10^3}\] tür.
Tabanları \(GFEH\) ve \(ABCD\) olan ve arada kalan eğik prizmanın yüksekliği de yukarıdaki şekillerde görüleceği üzere \(|TS|=40\) birim olacağından, hacmi \({10^2} \cdot 40\) olur. Böylece cismin toplam hacmi \[{10^2} \cdot 50\] olacaktır.
Daha geniş algı için aşağıdaki videoyu izleyebilirsiniz.
Bu cismi elde ederken gelme sırasını Ege, Irmak ve Çınar biçiminde kabul etmiştik. Oysa biliyoruz ki toplamda \(3! = 6\) farklı sıralama ile buluşma gerçekleşebilir. Bu da demektir ki bu cisimden \(6\) adet vardır. Aşağıdaki şekilde tüm cisimlerin videosunu gözlemleyebilirsiniz.
O halde istenilen olasılık \[P = \frac{{6 \cdot {{10}^2} \cdot 50}}{{{{60}^3}}} = \frac{5}{{36}}\] olarak bulunur.

