Örnek 1

Koordinat düzleminde \((0,0)\) noktasında başlayan iki tür hareket tanımlayalım:

\[S:(x,y) \to (x + 1,y)\] \[Y:(x,y) \to (x,y + 1)\]

S hareketinin 1 birim sağa ve Y hareketinin de 1 birim yukarı olduğunu görüyoruz. Bu hareketleri kullanarak \((0,0)\) noktasından \((5,5)\) noktasına kaç farklı biçimde gidebileceğimizi hesaplamak istersek, 5 adet S ve 5 adet Y kullanmamız gerektiğini görürüz. Bu durumda 5 adet S ve 5 adet Y harfinin her bir farklı sıralaması bir gidiş belirtecektir. O halde toplam gidiş sayısı \(\dfrac{{10!}}{{5! \cdot 5!}} = \left( {\begin{array}{*{20}{c}}
{10}\\5\end{array}} \right)\) kadardır. Şimdi kendimize bir kısıt getirelim ve herhangi bir hareketin \(y = x\) doğrusuna dokunabileceğini ama üstüne çıkamayacağını şart koşalım.

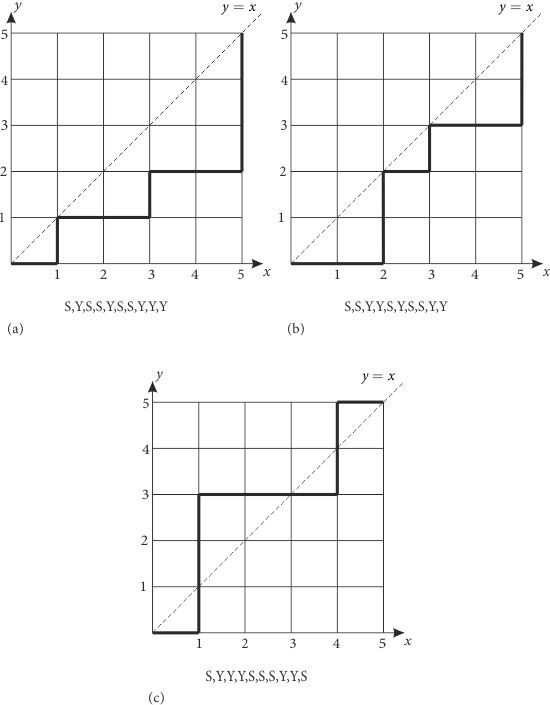
Yukarıdaki şekillerden (a) ve (b) koşulu sağlarken (c) sağlamamaktadır. Koşulumuzda ilk göze çarpan şey herhangi bir gidişin S ile başlayıp Y ile bitmesi gerektiğidir. Ayrıca herhangi bir noktaya kadar yapılan S sayısının Y sayısından az olmayacağı da (a) ve (b) şekillerden gözlemlenebilir. Yani herhangi bir gidişte \(S \ge Y\) dir. (c) şeklinde böyle bir durumun olmadığı da görülebilir. Bu durumların sayısı elde edebilmek için (c) deki gibi koşula uymayan yani \(y = x\) doğrusunun üstünde kalan yolların sayısını elde edip tüm durumdan çıkarabiliriz. (c) deki yolun ne zaman ilk olarak \(S \ge Y\) koşulunu bozduğu yerin 3. hareketten sonra olduğuna dikkate edin. Bunu hareket diziliminde bir çizgi ile gösterirsek

\[S,Y,Y{\rm{ }}|{\rm{ }}Y,S,S,S,Y,Y,S\]

olacaktır. Şimdi bu dizilime aşağıdaki gibi bir dönüşüm uygulayalım.

\[{\mathop{\rm S}\nolimits} ,Y,Y \,\,|\,\, Y,S,S,S,Y,Y,S \Leftrightarrow {\mathop{\rm S}\nolimits} ,Y,Y \,\,|\,\, S,Y,Y,Y,S,S,Y\]

Bu dönüşüm, koşulun bozulduğu ilk andan sonraki hareketleri birbiriyle değiştirmektedir. Yani Y yerine S, S yerine de Y hareketi seçilmektedir. Bu sayede hareket diziliminde 4 adet S ve 6 adet Y olmaktadır. (c) deki bu dönüşüm (d) şeklinde gösterilmektedir. Koşula aykırı bir diğer farklı yolda (e) şeklinde gösterilmektedir. Dönüşümle değişmiş biçimi de (f) de yer almaktadır. Yine 4 adet S ve 6 adet Y hareketi mevcuttur.

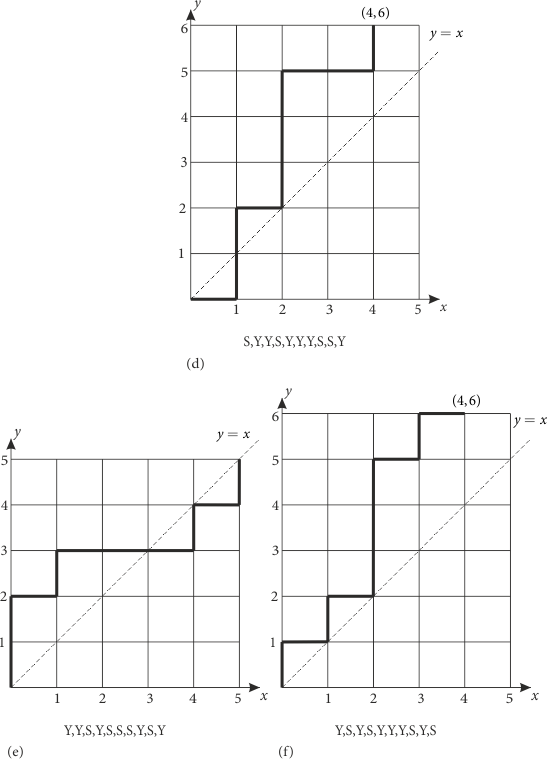
Şimdi 4 S ve 6 Y den oluşan bir hareket dizilimi olarak

\[S,Y,S,S,Y,Y,Y{\rm{ }}|{\rm{ }}Y,Y,S\]

dizilimine bakalım. Y lerin S lerden fazla olduğu ilk hareketten sonrasını çizgi ile ayırmış durumdayız. Bu dizilime dönüşüm uygularsak

\[S,Y,S,S,Y,Y,Y{\rm{ }}|{\rm{ }}S,S,Y\]

eldedilir. Dikkat ederseniz bu 5 S ve 5 Y den oluşan ama koşulumuza aykırı olan bir dizilimdir. Özetle uyguladığımız dönüşümle elde edilen her bir dizilim esasında koşula aykırı bir dizilime denktir. Yani bu biçimde \(\dfrac{{10!}}{{4! \cdot 6!}} = C(10,4)\) hareket dizilimi vardır. O halde koşula uygun

\[C(10,5) - C(10,6) = 42\]

gidiş vardır.

Yukarıdaki örnekle şöyle bir genelleme elde edebiliriz:

\(n \ge 0\) olmak üzere, \(y=x\) doğrusu üzerine çıkmadan \((0,0)\) noktasından \((5,5)\) noktasına \(n\) adet S ve \(n\) adet Y hareketi ile yapılabilecek yol sayısı

\[{b_n} = C(2n,n) - C(2n,n - 1) = \frac{1}{{n + 1}} \cdot C(2n,n), \quad n \ge 1, \quad b_0=1 \]

olur. \({b_0},{b_1},{b_2}, \cdot  \cdot  \cdot \) sayılarına ismini Belçikalı matematikçi Eugene Charles Catalan ‘dan alan Catalan sayıları denir. Eugene, bu sayıları \({x_1}{x_2}{x_3}...{x_n}\) çarpımını  kaç farklı biçimde paranteze alabileceğini hesaplamak için kullanmıştır. Örneğin \({x_1}{x_2}{x_3}{x_4}\) çarpımını \({b_3} = 5\) farklı biçimde paranteze alabiliriz:

\[\left( {\left( {\left( {{x_1}{x_2}} \right){x_3}} \right){x_4}} \right) \quad \left( {\left( {{x_1}\left( {{x_2}{x_3}} \right)} \right){x_4}} \right) \quad \left( {\left( {{x_1}{x_2}} \right)\left( {{x_3}{x_4}} \right)} \right) \quad \left( {{x_1}\left( {\left( {{x_2}{x_3}} \right){x_4}} \right)} \right) \quad  \left( {{x_1}\left( {{x_2}\left( {{x_3}{x_4}} \right)} \right)} \right) \]

Örnek 2

Yukarıdaki örnekle özünde aynı ama cümleleri değişik olan aşağıdaki örnekleri inceleyelim.

• 3 adet 1 ve 3 adet – 1 kullanarak elde edilen dizilimlerden \({b_3} = 5\) tanesinde herhangi bir sayıdan önceki sayıların toplamın negatif değildir.

  1, 1, 1, -1, -1, -1       1, 1, -1, -1, 1, -1       1, -1, 1, 1, -1, -1

  1, 1, -1, 1, -1, -1       1, -1, 1, -1, 1, -1

   

• 4 adet 1 ve 4 adet 0 kullanılarak elde edilen dizilimlerin \({b_4} = 14\) tanesinde, soldan sağa okunurken, 0 sayısı 1 sayısını geçmez.

  10101010    10101100    10110010

  10110100    10111000    11001010

  11001100    11010010    11010100

  11011000    11100010    11100100

  11101000    11110000

   

• (((ab(c)d)	(((abc	111000
  ((a(bc))d)	((a(bc	110100
  ((ab)(cd))	((ab(c	110010
  (a((bc)d))	(a((bc	101100
  (a(b(cd)))	(a(b(c	101010

  Tablonun 1.sütununda abcd çarpımının paranteze alınabilir biçimleri verilmiştir. İlk satırda yer alan (((ab(c)d) biçimini soldan sağa doğru okurken “)” parantezlerini görmezden gelerek 2.sütundaki (((abc dizilimini elde edebiliriz. Benzer biçimde ((a(bc))d) diziliminden ((a(bc elde edilecektir. Şimdi 2.sütundan bir dizilim alıp sonuna “d)” ekleyelim. Örneğin, 3.satırdaki ((ab(c dizilimi ile ((ab(cd) elde edilir. Soldan sağa doğru her bir ikili çarpımı “)” ile kapatırsak ((ab)(cd)) elde edilir. Dikkat ederseniz bu dizilim 1.sütundaki karşılığıdır.

  3.sütunun ne olduğu açık bir biçimde görülmektedir. “(“ sembollerini 1; a, b ve c harflerini de 0 sembolize etmektedir. O halde 1.sütunda yer alan her bir dizilime karşılık, 3 adet 1 ve 3 adet 0 içeren ve soldan sağa okunurken 0 sayısının 1 sayısından fazla olmadığı bir sayı dizisi karşılık gelmektedir. Bunların sayısının da \({b_3} = 5\) olduğu görülmektedir. O halde, genel olarak \({x_1}{x_2} \cdot \cdot \cdot {x_n}\) çarpımını \({b_{n - 1}}\) farklı biçimde paranteze alabilir.

• Şimdi, 1,2,3,4,5 ve 6 sayılarını 2 satır ve 3 sütundan oluşan bir tabloda (1) her bir satırda sayılar soldan sağa doğru okunurken küçükten büyüğe doğru dizili, (2) herhangi bir sütunda küçük sayı üstte olacak biçimde dizmeye çalışalım. Örneğin,

  1	2	4
  3	5	6

  Şimdi ilk satırda yer alan sayıları 1 ile ikinci satırda yer alan sayıları da 0 ile sembolize ederek tablodaki sayıların sırasına göre bir dizilim yaparsak \(123456 \leftrightarrow 110100\) elde ederiz. Şimdi tam tersi 0 sayısının 1 sayısını soldan sağa geçmediği rastgele bir dizilimi ele alıp tablo oluşturalım. Örneğin, \(101100 \leftrightarrow 123456\) ile

  1	3	4
  2	5	6

  elde edilir ki istenilen koşullara uygun bir tablomuz olur. O halde bu sorunun cevabı da \({b_3} = 5\) olacaktır.