- Eşkenar Üçgen - 05/05/2017
- İntegral - 01/04/2016
- İntegral - 10/05/2015
- Kareler 06/01/2015
- Labirent 12/07/2014
- Elips ve Teğetleri 04/07/2014
- İntegral 20/06/2014
- Elips içinde üçgen 28/03/2014
- Mutlak Değer 20/03/2014
- Çemberlere Eşit Uzaklık 03/03/2014
- Köyler arası yollar 23/02/2014
- Ardışık yazılımlar 16/02/2014
- Kombinasyon Özdeşliği 10/02/2014
- Üç kişinin buluşması 25/01/2014
- Parabolün dik teğetleri 05/01/2014
- Bir açı sorusu 24/11/2013
- Alt küme elemanlar çarpımı 07/11/2013
- Kare ve Çemberler 30/10/2013
- Bir cebir sorusu 30/10/2013
- Dörtgen oluşturma olasılığı 01/06/2013
Soru
Herhangi bir eşkenar üçgeni eşit alanlı iki bölgeye ayıran ve uç noktaları eşkenar üçgen üzerinde bulunan doğru parçalarının orta noktalarının geometrik yerinin belirttiği kapalı bölgenin alanının eşkenar üçgenin alanına oranını hesaplayınız.Çözüm
Soru
Aşağıdaki integralleri hesaplayınız.- $$\int\limits_{ - \pi/4}^{3\pi/4} {\left( {{{\cos }^2}\left( {\sin x} \right) + {{\sin }^2}\left( {\cos x} \right)} \right)dx} $$
- $$\int {\frac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} $$
Çözüm
- Birinci soru,
1.Çözüm
$$A = \int\limits_{ - \pi /4}^{3\pi /4} {\left( {{{\cos }^2}(\sin x) + {{\sin }^2}(\cos x)} \right)dx} $$ olsun. $u = \dfrac{\pi }{2} - x$ dönüşümü yapılırsa, $$A = \int\limits_{ - \pi /4}^{3\pi /4} {\left( {{{\cos }^2}(\cos u) + {{\sin }^2}(\sin u)} \right)du} $$ elde edilir. Bu iki integral toplanır ve ${\sin ^2}x + {\cos ^2}x = 1$ özdeşliği göz önüne alınırsa, $$2A = \int\limits_{ - \pi /4}^{3\pi /4} {2dx} = 2\pi $$ olur. O halde, $$A = \pi $$ olur.
2.Çözüm
Öncelikle $${\sin ^2}a - {\sin ^2}b = \sin \left( {a - b} \right)\sin \left( {a + b} \right)$$ $$\cos x - \sin x = - \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right)$$ $$\cos x + \sin x = \sqrt 2 \cos \left( {x - \frac{\pi }{4}} \right)$$ özdeşliklerini kullanacağız. Böylece, $$\begin{align*} {\cos ^2}\left( {\sin x} \right) + {\sin ^2}\left( {\cos x} \right) & = 1 - {\sin ^2}\left( {\sin x} \right) + {\sin ^2}\left( {\cos x} \right) \\ & = 1 - \sin \left( {\cos x - \sin x} \right)\sin \left( {\cos x + \sin x} \right) \\ & = 1 + \sin \left( {\sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right)} \right)\sin \left( {\sqrt 2 \cos \left( {x - \frac{\pi }{4}} \right)} \right) \end{align*}$$ olur.
$u = x - \dfrac{\pi }{4}$ dönülümü uygulanırsa,
$$\begin{align*} \int\limits_{ - \pi /4}^{3\pi /4} {\left( {{{\cos }^2}\left( {\sin x} \right) + {{\sin }^2}\cos x} \right)dx} & = \int\limits_{ - \pi /2}^{\pi /2} {\left( {1 + \underbrace {\sin \left( {\sqrt 2 \sin u} \right)\sin \left( {\sqrt 2 \cos u} \right)}_{tek\,\,fonksiyondur}} \right)du} \\ & = \int\limits_{ - \pi /2}^{\pi /2} {1du} \\ & = \pi \end{align*}$$ elde edilir.
- İkinci soru,
1.Çözüm: (Hasan BOSTANLIK)
$$\int {\frac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} = \int {\underbrace {\frac{x}{{\cos x}}}_u\underbrace {\frac{{x\cos x}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx}_{dv}} $$ olsun. Bu durumda, $v = - \dfrac{1}{{x\sin x + \cos x}}$ ve $du = \dfrac{{x\sin x + \cos x}}{{{{\cos }^2}x}}dx$ olacaktır. Kısmi integral alınırsa, $$\int {\frac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} = - \frac{x}{{\cos x\left( {x\sin x + \cos x} \right)}} + \int {\frac{1}{{{{\cos }^2}x}}dx} $$ $$\int {\frac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} = - \frac{x}{{\cos x\left( {x\sin x + \cos x} \right)}} + \frac{{\sin x}}{{\cos x}} + C$$ olur. Sağ tarafta payda eşitlenir ve pay kısmı x parantezine alınırsa, $$\int {\frac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} = \frac{{\sin x - x\cos x}}{{x\cos x + \sin x}} + C$$ sonucuna ulaşılır.
2.Çözüm
Öncelikle, $$d\left( {\frac{u}{v}} \right) = d\left( {u.\frac{1}{v}} \right) = \frac{1}{v}du - \frac{u}{{{v^2}}}dv$$ olacağından, $$\int {\frac{1}{v}du} = \frac{u}{v} + \int {\frac{u}{{{v^2}}}dv} $$ kısmi integral yapısını $\int {\dfrac{{x\sin x}}{{x\sin x + \cos x}}dx} $ integralinde kullanalım.
$$\int {\underbrace {\frac{1}{{x\sin x + \cos x}}}_{1/v}\underbrace {x\sin xdx}_{du}} = \frac{{\sin x - x\cos x}}{{x\sin x + \cos x}} + \int {\frac{{\left( {\cos x - \sin x} \right)x\cos x}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} $$ olur. Böylece, $$ \int {\frac{{x\sin x}}{{x\sin x + \cos x}}dx} - \int {\frac{{\left( {\cos x - \sin x} \right)x\cos x}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} = \frac{{\sin x - x\cos x}}{{x\sin x + \cos x}} + C$$ elde edilir. Sol tarafta yer alan iki integral tek integral içinde işleme alınırsa, $$\int {\frac{{{x^2}}}{{{{\left( {x\sin x + \cos x} \right)}^2}}}dx} = \frac{{\sin x - x\cos x}}{{x\sin x + \cos x}} + C$$ sonucuna ulaşılır.
Soru
\(k\) bir pozitif tam sayı olmak üzere, \[\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \left( {\begin{array}{*{20}{c}}{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}\] olduğunu gösteriniz.
Kaynak: IB High Level Paper 1 2013 Aralık (Sabah) Soru 12 (Sorunun son aşamasında istenen genellemedir. Soru doğrudan doğruya bu ispatla başlamamaktadır. Bu kadar zor sanmayın:) )
Çözüm
$z = \cos x + i \cdot \sin x$ için ${z^{ - 1}} = \cos (x) - i \cdot \sin (x)$ olacağından, \[z + {z^{ - 1}} = 2{\mathop{\rm cosx}\nolimits} \] dir. Bu durumda, \[{(z + {z^{ - 1}})^{2k}} = {2^{2k}} \cdot {\cos ^{2k}}x \quad (1)\] olur. Öte yandan sol tarafa binom açılımı uygulanırsa, \[{(z + {z^{ - 1}})^{2k}} = \sum\limits_{r = 0}^{2k} {\left( {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right){z^{2k - r}} \cdot {z^{ - r}}} \right)} = \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right){z^{2(k - r)}}} \quad (2)\] dir.
Bu ifadede, ${z^{2(k - r)}} = \cos \left( {2(k - r)x} \right) + i \cdot \sin \left( {2(k - r)x} \right)$ dikkate alınır ve $(1)$ ve $(2)$ birlikte düşünülürse, \[{2^{2k}} \cdot {\cos ^{2k}}x = \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\cos \left( {2(k - r)x} \right)} + i \cdot \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\sin \left( {2(k - r)x} \right)} \] olur. Karmaşık sayıların eşitliği gereği, sol tarafta sanal kısım olmadığından, $\sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\sin \left( {2(k - r)x} \right)} = 0$ dır.
Böylece, \[{2^{2k}} \cdot {\cos ^{2k}}x = \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\cos \left( {2(k - r)x} \right)} \quad (3) \] olur. Dikkat edilirse $k \ne r$ için, \[\int\limits_0^{\frac{\pi }{2}} {\cos (2(k - r) \cdot x)} dx = \left. {\left( {\frac{1}{{2(k - r)}}\sin (2(k - r) \cdot x)} \right)} \right|_0^{\frac{\pi }{2}} = 0 \quad (4)\] dir.
$k = r$ için ise, \[\int\limits_0^{\frac{\pi }{2}} {\cos (2(k - r) \cdot x)} dx = \int\limits_0^{\frac{\pi }{2}} {1 \cdot } dx = \frac{\pi }{2} \quad (5)\] dir.
Bu durumda, $(3)$ te her iki tarafın da $0$ dan $\dfrac{\pi }{2}$ ye integrali alınırsa, \[{2^{2k}} \cdot \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{2}\] elde edilir. Böylece, \[\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}\] bulunur.
Çözüm (Ayhan Yanağlıbaş)
Verilen önermenin ispatını tümevarım yöntemi ile gösterelim. \[D(k){\rm{ }} = {\rm{ }}\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}} \] olmak üzere,
\[\begin{align*}
D(1) & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^2}xdx} \\
& = \int\limits_0^{\frac{\pi }{2}} {\left( {\frac{{1 + \cos 2x}}{2}} \right)dx} \\
& = \left. {\left[ {\frac{x}{2} + \frac{{\sin 2x}}{4}} \right]} \right|_0^{\frac{\pi }{2}}\\
& = \frac{\pi }{4} = \left( {\begin{array}{*{20}{c}}
2\\
1
\end{array}} \right) \cdot \frac{\pi }{{{2^3}}}
\end{align*}\]
doğrudur. Şimdide, \[D(k) = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}} \quad (1) \] önermesinin doğruluğunu kabul edip, \[D(k + 1) = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k + 2}}xdx = \left( {\begin{array}{*{20}{c}}
{2k + 2}\\
{k + 1}
\end{array}} \right).\frac{\pi }{{{2^{2k + 3}}}}} \quad (2)\] önermesinin doğruluğunu gösterelim. Bunun için \[\int {{{\cos }^n}xdx = } \frac{1}{n}\sin x{\cos ^{n - 1}}x + \frac{{n - 1}}{n}\int {{{\cos }^{n - 2}}xdx}\] indirgeme formülünden yararlanacağız. Bu formüle göre, \[\begin{align*}
D(k + 1) & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k + 2}}xdx} \\
& = \overbrace {\left. {\left( {\frac{1}{{2k + 2}}\sin x{{\cos }^{(2k + 1)}}x} \right)} \right|_0^{\frac{\pi }{2}}}^U + \overbrace {\frac{{2k + 1}}{{2k + 2}} \cdot \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} }^V
\end{align*}\] yazılabilir. \[u = \left. {\left( {\frac{1}{{2k + 2}} \cdot \sin x{{\cos }^{(2k + 1)}}x} \right)} \right|_0^{\frac{\pi }{2}} = {\rm{ }}0\] olur. Ayrıca, $v$ ifadesinde $(1)$ numaralı eşitlik kullanılırsa, \[v = \frac{{2k + 1}}{{2k + 2}} \cdot \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \frac{{2k + 1}}{{2k + 2}} \cdot \left( {\begin{array}{*{20}{c}}
{2k}\\
{k}
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k+1}}}}\] dir. \[\begin{align*}
D(k + 1) & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k + 2}}xdx} \\
& = v\\
& = \dfrac{{2k + 1}}{{2k + 2}} \cdot \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \dfrac{\pi }{{{2^{2k + 1}}}}\\
& = \dfrac{{2k + 1}}{{2(k + 1)}} \cdot \dfrac{{(2k)!}}{{k!.k!}} \cdot \dfrac{\pi }{{{2^{2k + 1}}}}
\end{align*}\] eşitliği $\dfrac{{2k + 2}}{{2(k + 1)}}$ ile genişletirsek, \[\begin{align*}
D(k + 1) & = \dfrac{{2k + 2}}{{2(k + 1)}} \cdot \dfrac{{2k + 1}}{{2(k + 1)}} \cdot \dfrac{{(2k)!}}{{k!.k!}} \cdot \dfrac{\pi }{{{2^{2k + 1}}}}\\
& = \dfrac{{(2k + 2)!}}{{(k + 1)!(k + 1)!}} \cdot \dfrac{\pi }{{4 \cdot {2^{2k + 1}}}}\\
& = {\rm{ }}\left( {\begin{array}{*{20}{c}}
{2k + 2}\\
{k + 1}
\end{array}} \right) \cdot \dfrac{\pi }{{{2^{2k + 3}}}}
\end{align*}\] olur. Böylece (2) numaralı eşitlik doğrulanmış olur. Tümevarım gereği ispat tamamlanmıştır.
Çözüm (Adem Çil)
Verilen integral, \[\begin{align*}
{I_{2k}} & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} \\
& = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x(1 - {{\sin }^2}x)dx} \\
& = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}xdx} - \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x{{\sin }^2}xdx} \\
& = {I_{2k - 2}} - \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x{{\sin }^2}xdx}
\end{align*}\] olur. \[\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x{{\sin }^2}xdx} = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x\sin x \cdot \sin xdx} \] yazılır ve \[u = \sin x \Rightarrow dx = \cos xdx\] \[dv = {\cos ^{2k - 2}}x\sin xdx \Rightarrow v = - \frac{1}{{2k - 1}}{\cos ^{2k - 1}}x\] ile kısmi integral alınırsa, \[\begin{align*}
{I_{2k}} & = {I_{2k - 2}} - \left[ {\left. {\left( {\frac{1}{{2k - 1}}{{\cos }^{2k - 1}}x\sin x} \right)} \right|_0^{\frac{\pi }{2}} + \frac{1}{{2k - 1}}\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} } \right]\\
& = {I_{2k - 2}} - \frac{1}{{2k - 1}} \cdot {I_{2k}}
\end{align*}\] olur. Bu eşitlikten, ${I_{2k}} = \left( {\frac{{2k - 1}}{{2k}}} \right) \cdot {I_{2k - 2}}$ indirgemesine ulaşırız. O halde, \[{I_{2k}} = \frac{{2k - 1}}{{2k}} \cdot \frac{{2k - 3}}{{2k - 2}} \cdot \cdot \cdot \frac{3}{4} \cdot {I_2}\] olur. ${I_2} = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^2}xdx} = \frac{\pi }{4}$ yerine yazılırsa, \[{I_{2k}} = \frac{{2k - 1}}{{2k}} \cdot \frac{{2k - 3}}{{2k - 2}} \cdot \cdot \cdot \frac{3}{4} \cdot \frac{\pi }{4}\] olur. Payda 2 parantezine alınırsa, \[\begin{align*}
{I_{2k}} & = \frac{{2k - 1}}{k} \cdot \frac{{2k - 3}}{{k - 1}} \cdot \cdot \cdot \frac{3}{2} \cdot \frac{\pi }{{{2^{k + 1}}}}\\
& = \frac{{(2k - 1)(2k - 3) \cdot \cdot \cdot 3}}{{k!}} \cdot \frac{\pi }{{{2^{k + 1}}}} \end{align*}\] olur. Eşitliğin sağ tarafında pay ve paydayı $2k(2k - 2)(2k - 4) \cdot \cdot \cdot 2 = {2^k} \cdot k!$ ile çarparsak, \[\begin{align*}
{I_{2k}} & = \frac{{2k(2k - 1)(2k - 2)(2k - 3) \cdot \cdot \cdot 3 \cdot 2}}{{{2^k}k! \cdot k!}} \cdot \frac{\pi }{{{2^{k + 1}}}}\\
& = \frac{{(2k)!}}{{k! \cdot k!}} \cdot \frac{\pi }{{{2^{2k + 1}}}}\\
& = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}
\end{align*}\] ile kanıt tamamlanır.
Soru

Şekilde, ABC üçgeninin kenarlarını ortak kenar kabul eden kareler çizilmiştir.
$\left| {JG} \right| = a$ birim, $\left| {HL} \right| = b$ birim ve $\left| {ON} \right| = c$ birim olduğuna göre, karelerin alanları toplamının
\[\frac{{{a^2} + {b^2} + {c^2}}}{3}\]
birim kare olduğunu gösteriniz.
Çözüm
13/01/2015 tarihinde verilecektir.
Soru
Düzgün sekizyüzlü biçimindeki bir labirentin herhangi bir köşesine bırakılan bir fare ayrıtlar üzerinde hareket ederek bırakıldığı bu köşenin karşı köşesine vardığında labirentten çıkmış oluyor. Farenin bir köşeden diğer bir köşeye gitme süresi $t$ saat olduğuna göre, labirentten ortalama çıkma süresini $t$ cinsinden bulunuz.(Soru metninde açık olsada tereddüte yer vermemek adına belirtmem gerekir ki, fare ilk bırakıldığı köşeye tekrar tekrar gelebilir, yani gittiği bir yoldan tekrar geri dönebilir.)
Çözüm
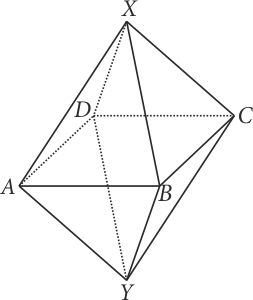
Şekildeki gibi bir sekizyüzlü düşünelim. Faremiz $X$ noktasına bırakılsın. Dolayısıyla $Y$ noktasına geldiğinde labirentten çıkmış olacaktır. Farenin $X$ noktasındayken labirentten ortalama çıkma (labirentten ortalama kurtulma) süresine $x$ diyelim. Benzer biçimde, fare $A$ noktasındayken labirentten ortalama çıkma süresine de $a$ diyelim. Dikkat edilirse, $B$, $C$ ve $D$ noktaları için de ortalama çıkma süresi $A$ noktası ile aynı yani $a$ olacaktır. Tekrar $X$ noktasına geri dönelim. Bu noktadan $\dfrac{1}{4}$ er ihtimalle $A$, $B$, $C$ ve $D$ noktalarına gidebilir. O halde, \[x = \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) = a + t\] dir. Eklenen $t$ süreleri $X$ den diğer noktalara geçmek için kullanılan ayrıtlardan kaynaklanmaktadır. Şimdi aynı mantıkta $A$ noktasını düşünelim.
- $\dfrac{1}{4}$ olasılıkla $B$ ye gidebilir. Ayrıtta geçen $t$ süre ve $B$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + t)$ olur.
- $\dfrac{1}{4}$ olasılıkla $D$ ye gidebilir. Ayrıtta geçen $t$ süre ve $D$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + t)$ olur.
- $\dfrac{1}{4}$ olasılıkla $X$ e gidebilir. Ayrıtta geçen $t$ süre ve $X$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + 2t)$ olur.
- $\dfrac{1}{4}$ olasılıkla $Y$ ye gidebilir. Ayrıtta geçen $t$ süre eklenince: $\dfrac{1}{4}(t)$ olur.
O halde, $A$ noktasından ortalama çıkma süresi \[a = \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + 2t} \right) + \frac{1}{4}t\] dir. Bu denklemden \[a = 5t\] bulunur. Böylece, \[x = a + t = 5t + t = 6t\] elde edilir.
Soru
Denklemi \[\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\] olan elipsin, $\alpha$ ölçüyle kesişen teğetlerinin kesim noktalarının geometrik yerinin \[\frac{{\tan \alpha }}{2} = \frac{{\sqrt {{x^2}{y^2} - ({x^2} - {a^2})({y^2} - {b^2})} }}{{{x^2} + {y^2} - {a^2} - {b^2}}}\] olduğunu gösteriniz. ( $\alpha = {90^ \circ }$ için bu denklemin elipsin Monge çemberini verdiğine dikkat ediniz.)Çözüm (Hatice Mankan)
Elipsin birbirini $\alpha$ ölçüyle kesen teğetlerinin genel denklemi $y=mx+n$ ve bu teğetlerin kesim noktası $P(h,k)$ olsun. Noktayı denklemde yerine yazarsak, $n=k-mh$ olur. Böylece doğruların denklemi \[y=mx+k-mh\] olur. Elips ile ona teğet olan doğrunun ortak çözümünden gelen teğetlik şartı formülününün $a^2m^2+b^2-n^2=0$ olduğunu hatırlar ve sorumuzda kullanırsak: \begin{array}{l} \\ & {a^2}{m^2} + {b^2} - {(k - mh)^2} = 0 \\ & \Rightarrow {m^2}({a^2} - {h^2}) + m(2kh) + {b^2} - {k^2} = 0 \end{array} $m$ ye bağlı ikinci derece denklemi elde ederiz. Elipsin teğetleri arasındaki açının ölçüsü $\alpha$ olduğuna göre, iki doğru arasındaki açıya dair \[\tan \alpha = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|\] formülü kullanabiliriz. Elde ettiğimiz $m$ ye bağlı ikinci derece denklemin kökleri arasında \[{m_1}{m_2} = \frac{{{b^2} - {k^2}}}{{{a^2} - {h^2}}} \quad {m_1} - {m_2} = \frac{{\sqrt \Delta }}{{\left| a \right|}} = \frac{{2\sqrt {{h^2}{k^2} - ({a^2} - {h^2})({b^2} - {k^2})} }}{{\left| {{a^2} - {h^2}} \right|}}\] eşitliklerini yerine yazarsak \[\tan \alpha = \left| {\frac{{\frac{{2\sqrt {{h^2}{k^2} - ({a^2} - {h^2})({b^2} - {k^2})} }}{{\left| {{a^2} - {h^2}} \right|}}}}{{1 + \frac{{{b^2} - {k^2}}}{{{a^2} - {h^2}}}}}} \right| = 2\frac{{\sqrt {{h^2}{k^2} - ({a^2} - {h^2})({b^2} - {k^2})} }}{{\left| {{a^2} + {b^2} - {h^2} - {k^2}} \right|}}\] elde edilir. Böylece \[\frac{{\tan \alpha }}{2} = \frac{{\sqrt {{h^2}{k^2} - ({a^2} - {h^2})({b^2} - {k^2})} }}{{\left| {{a^2} + {b^2} - {h^2} - {k^2}} \right|}}\] elde edilir. Seçtiğimiz kesim noktası $P(h,k)$ geometrik yeri ifade ettiğinden, $h=x$ ve $k=y$ yerine yazılırsa \[\frac{{\tan \alpha }}{2} = \frac{{\sqrt {{x^2}{y^2} - ({x^2} - {a^2})({y^2} - {b^2})} }}{{\left| {{a^2} + {b^2} - {x^2} - {y^2}} \right|}}\] denklemiyle istenilen geometrik yer elde edilmiş olur. Eşitlikte mutlak değer yer almasının temel nedeni doğrular arasındaki açının dar veya geniş olmasından kaynaklıdır.
Soru
$n \in {N^+}$, $f\left( x \right) = \left( {x - 1} \right)\left( {x - 2} \right) \cdot \cdot \cdot \left( {x - n} \right)$ ve $g(x) = \sum\limits_{k = 1}^n {\dfrac{{f\left( x \right)}}{{x - k}}} $ olduğuna göre, \[\int\limits_0^{n + 1} {g\left( x \right)dx} \] integralinin $n$ tam sayısının çift değerleri için $0$; tek değerleri için $2n!$ olduğunu gösteriniz.Çözüm
Belirli integralin sınır değerlerini yerine yazmadan önce, mevcut integrale belirsiz biçimde yaklaşarak kuralı elde edelim (+c sabitleri ihmal edilmiştir). Öncelikle, \[g(x) = \sum\limits_{k = 1}^n {\frac{{f(x)}}{{x - k}}} = f(x) \cdot \left( {\frac{1}{{x - 1}} + \frac{1}{{x - 2}} + ... + \frac{1}{{x - n}}} \right)\] olacaktır. Bu eşitlikte \[\frac{1}{{x - 1}} + \frac{1}{{x - 2}} + ... + \frac{1}{{x - n}} = h(x)\] alınırsa, $g(x) = f(x) \cdot h(x)$ dir. Bu durumda, $\displaystyle \int {g(x)dx} = \int {f(x)h(x)dx} $ olur. Kısmi integral uygulayalım: $f(x) = u$ ve $h(x)dx = dv$ olsun. $f'(x)dx = du$ ve $v = \ln \left( {\left( {x - 1} \right) \cdot \left( {x - 2} \right)...\left( {x - n} \right)} \right) = {\mathop{\rm lnf}\nolimits} (x)$ olur. Böylece, \[\int {f(x)h(x)dx} = f(x) \cdot \ln f(x) - \int {\ln \left( {f(x)} \right)f'(x)dx} \] olur. Sağ tarafta kalan integralde tekrar kısmi integral alalım. $\ln f(x) = u$ ve $f'(x)dx = dv$ olursa; $\dfrac{{f'(x)}}{{f(x)}}dx = du$ ve $f(x) = v$ olur. Yerine yazılırsa, \[\int {\ln \left( {f(x)} \right)f'(x)dx} = f(x) \cdot \ln f(x) - \int {f(x)\frac{{f'(x)}}{{f(x)}}dx} = f(x) \cdot \ln f(x) - f(x)\] elde edilir. Böylece, \[\int {f(x)h(x)dx} = f(x) \cdot \ln f(x) - \left( {f(x) \cdot \ln f(x) - f(x)} \right) = f(x)\] bulunur. O halde, \[\int\limits_0^{n + 1} {g(x)dx} = \left. {f(x)} \right|_0^{n + 1} = f(n + 1) - f(0)\] olur. $n$ nin çift olması durumunda \[f(n + 1) = f(0) = n!\] olacağından \[\int\limits_0^{n + 1} {g(x)dx} = 0\] olur. $n$ nin tek olması durumunda ise, \[f(n + 1) = n!\ \quad \quad f(0) = - n!\] olacağından \[\int\limits_0^{n + 1} {g(x)dx} = 2n!\] bulunur. (Soruda $f$ fonksiyonunun türevinin bir başka biçiminin $g$ fonksiyonunun en sade hali olduğu anlaşılmaktadır. Sorunun kurgusunuda bu gerçek üzerine yapmıştım.)
Soru
Köşeleri, \[\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\] elipsi üzerinde bulunan üçgenlerden alanı en büyük olanının alanının \[\dfrac{3\sqrt{3}ab}{4}\] olduğunu gösteriniz. (Soru kitle olarak üniversite öğrencilerine yöneliktir. Lise seviyesinde 12.sınıflar türev kullanarak üçgenleri ikizkenar kabul ederek çözüm üretebilirler. Formül aynı olacaktır.)Çözüm
Üçgenin köşelerine \(A({x_1},{y_1})\), \(B({x_2},{y_2})\) ve \(C({x_3},{y_3})\) diyelim. Elipsin parametrik denkleminden faydalanırsak, \(0 \le \alpha ,\theta ,\beta < 2\pi \) için \[\begin{array}{l} {x_1} = a\cos \alpha \\ {y_1} = b\sin \alpha \end{array} \quad \begin{array}{l} {x_2} = a\cos \theta \\ {y_2} = b\sin \theta \end{array} \quad \begin{array}{l} {x_3} = a\cos \beta \\ {y_3} = b\sin \beta \end{array} \] olur. \(ABC\) üçgeninin alanı için \[\overrightarrow {AB} = (a(\cos \theta - \cos \alpha ),b(\sin \theta - \sin \alpha ))\] ve \[\overrightarrow {AC} = (a(\cos \beta - \cos \alpha ),b(sin\beta - sin\alpha ))\] vektörlerini kullanabiliriz.
Hatırlatma: \(\overrightarrow u = (a,b)\) ve \(\overrightarrow v = (x,y)\) vektörleri üzerine kurulu üçgensel bölgenin alanı
\[\frac{1}{2} \cdot \left| {\left| {\begin{array}{*{20}{c}}
a&b\\
x&y
\end{array}} \right|} \right| = \frac{{\left| {ay - bx} \right|}}{2}\] dir.
O halde,
\[|ABC| = \frac{1}{2} \cdot \left| {\left| {\begin{array}{*{20}{c}}
{a(\cos \theta - \cos \alpha )}&{b(\sin \theta - sin\alpha )}\\
{a(\cos \beta - \cos \alpha )}&{b(\sin \beta - \sin \alpha )}
\end{array}} \right|} \right|\] olur. Bu denklem düzenlenirse, \[|ABC| = \frac{{ab \cdot \left| {\sin (\beta - \theta ) + \sin (\theta - \alpha ) + \sin (\alpha - \beta )} \right|}}{2}\] elde edilir. \(\beta - \theta = u\), \(\theta - \alpha = v\) ve \(\alpha - \beta = w\) değişikliği yaparsak ve \(u + v + w = 0\) olduğunu görürsek, \[|ABC| = \frac{{ab \cdot \left| {\sin u + \sin v - \sin (u + v)} \right|}}{2}\] olur. (Bu değişiklikte \( - 2\pi < u,v,w < 2\pi \) olacağına dikkat ediniz). Bu durumda üçgenin alanı \[F(u,v) = \sin u + \sin v - \sin (u + v)\] fonksiyonuna bağlı olur. Bu fonksiyonun maksimum değerini bulmak için \[{F_u}(u,v) = \cos u - \cos (u + v) = 0 \quad {F_v}(u,v) = \cos v - \cos (u + v) = 0\] denklemleri ortak çözülürse, \(\cos u = \cos v\) yani \(u=v\) veya \(u=-v\) olmalıdır. Eğer \(u=-v\) olursa, \({F_u}(u,v) = \cos u - \cos (u - u) = 0\) olacağından \(u=0=v\) olur. Eğer \(u=v\) olursa, \({F_u}(u,v) = \cos u - \cos (2u) = 0\) olacağından \(u = v = \dfrac{{2\pi }}{3}\), \(u = v = \dfrac{{4\pi }}{3}\) ve \(u=v=0\) elde edilir. \(F(0,0) = 0\) olduğundan üçgenin alanı 0 olmak zorunda kalır. Diğer noktalar için çift değişkenli fonksiyonlarda ekstremum değerler için varolan teoremi* kullanmamız gerekiyor. Ekstremum testi için, \({F_{uu}}(u,v) = - \sin u + \sin (u + v)\), \({F_{vv}}(u,v) = - \sin v + \sin (u + v)\) ve \({F_{uv}}(u,v) = \sin (u + v)\) değerlerinde \(\left( {\dfrac{{2\pi }}{3},\dfrac{{2\pi }}{3}} \right)\) ve \(\left( {\dfrac{{4\pi }}{3},\dfrac{{4\pi }}{3}} \right)\) noktalarını araştırmamız gerekiyor. \[{F_{uu}}\left( {\dfrac{{2\pi }}{3},\dfrac{{2\pi }}{3}} \right) = - \sqrt 3 \] \[{F_{vv}}\left( {\dfrac{{2\pi }}{3},\dfrac{{2\pi }}{3}} \right) = - \sqrt 3 \] \[{F_{uv}}\left( {\dfrac{{2\pi }}{3},\dfrac{{2\pi }}{3}} \right) = - \frac{{\sqrt 3 }}{2}\] olur. Burada \({F_{uu}} < 0\) ve \({F_{uu}} \cdot {F_{vv}} - {F_{uv}}^2 = 3 - \dfrac{3}{4} = \dfrac{9}{4} > 0\) olduğundan teorem* gereği bu nokta bir maksimum noktadır. Benzer biçimde \(\left( {\dfrac{{4\pi }}{3},\dfrac{{4\pi }}{3}} \right)\) noktası da minimum nokta olacaktır. O halde fonksiyon maksimum değerini \(u = v = \dfrac{{2\pi }}{3}\) için alır. \[F\left( {\dfrac{{2\pi }}{3},\dfrac{{2\pi }}{3}} \right) = \dfrac{{\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2} - \left( { - \frac{{\sqrt 3 }}{2}} \right) = \dfrac{{3\sqrt 3 }}{2}\] olur. Böylece üçgenin alanının maksimum değeri, \(|ABC| = \dfrac{{3\sqrt 3 ab}}{4}\) bulunur. ( Dikkat edilirse, alandaki mutlak değerden dolayı \(\left( {\dfrac{{4\pi }}{3},\dfrac{{4\pi }}{3}} \right)\) değerleri içinde alan aynı çıkacaktır.)
Yardımcı Teorem:
\(F(u,v)\) fonksiyonu ile birinci ve ikinci türevlerinin \((a,b)\) noktasında sürekli ve \({F_u}(a,b) = {F_v}(a,b) = 0\) olsun. Bu durumda
\(F(u,v)\) fonksiyonu ile birinci ve ikinci türevlerinin \((a,b)\) noktasında sürekli ve \({F_u}(a,b) = {F_v}(a,b) = 0\) olsun. Bu durumda
- Eğer \({F_{uu}} < 0\) ve \({F_{uu}} \cdot {F_{vv}} - {F_{uv}}^2 > 0\) ise, \(F\) fonksiyonunun \((a,b)\) noktasında yerel maksimumu vardır.
- Eğer \({F_{uu}} > 0\) ve \({F_{uu}} \cdot {F_{vv}} - {F_{uv}}^2 > 0\) ise, \(F\) fonksiyonunun \((a,b)\) noktasında yerel minimumu vardır.
- Eğer \({F_{uu}} \cdot {F_{vv}} - {F_{uv}}^2 < 0\) ise, \((a,b)\) noktası semer noktasıdır (saddle point).
- Eğer \({F_{uu}} \cdot {F_{vv}} - {F_{uv}}^2 = 0\) ise, bu teorem bir yorum üretmez, farklı yöntemlerle incelemek gerekir.
Aşağıdaki şekilde \(\alpha\) açısını değiştirerek üçgeni hareket ettirebilirsiniz.
Soru
\(a\),\(b\), \(c\), \(d\) ve \(e\) birer reel sayı olmak üzere, \[|a \pm |bx + c|| = dx + e\] denkleminin olası köklerinin \[{x_{1,2}} = - \frac{{c + e \pm a}}{{b + d}}\quad \quad {x_{3,4}} = - \frac{{c - e \pm a}}{{b - d}}\] olduğunu gösteriniz. (Eğer katsayılar birer rasyonel sayı ise, köklerin de rasyonel olduğu görülmektedir.)Çözüm
Soruda geçen \(\pm\) yerine \(+\) kullanarak çözüm vereceğim. \(-\) için çözümü ilgililer yapabilir.
Öncelikle \[|a + |bx + c|| = dx + e\] denkleminin ilk mutlak değerinden kurtulalım: \[|bx + c| = dx + e-a\] veya \[|bx + c| = -dx - e-a\] olur. Her iki tarafında karesini alarak ikinci mutlak değerden kurtulalım: \[{b^2}{x^2} + 2bcx + {c^2} = {d^2}{x^2} + 2d(e - a)x + {(e - a)^2}\] veya \[{b^2}{x^2} + 2bcx + {c^2} = {d^2}{x^2} + 2d(e + a)x + {(e + a)^2}\] olur. Düzenlersek, \[({b^2} - {d^2}){x^2} + 2[bc - d(e - a)]x + {c^2} - {(e - a)^2} = 0 \quad (1)\] veya \[({b^2} - {d^2}){x^2} + 2[bc - d(e + a)]x + {c^2} - {(e + a)^2} = 0 \quad (2)\] elde edilir. \((1)\) nolu denklemde \(({b^2} - {d^2}){x^2}\) ifadesini
\[\begin{array}{l}
(b + d)x\\
(b - d)x
\end{array}\] biçiminde, \({c^2} - {(e - a)^2}\) ifadesini de
\[\begin{array}{l}
c + (e - a)\\
c - (e - a)
\end{array}\] biçiminde ayırıp çapraz çarpımı gerçekleştirirsek denklemin orta terimi olan \[2[bc - d(e - a)]x\] ifadesini elde ederiz. O halde \((1)\) nolu denklemin çarpanlara ayrılmış biçimi \[[(b + d)x + c + e - a] \cdot [(b - d)x + c - e + a] = 0\] olur. Bu ifadeden denklemin olası kökleri \[{x_1} = - \frac{{c + e - a}}{{b + d}} \quad {x_2} = - \frac{{c - e + a}}{{b - d}}\] olur.
Benzer biçimde \((2)\) nolu denklemde, \(({b^2} - {d^2}){x^2}\) ifadesini
\[\begin{array}{l}
(b + d)x\\
(b - d)x
\end{array}\] biçiminde, \({c^2} - {(e + a)^2}\) ifadesini de
\[\begin{array}{l}
c + (e + a)\\
c - (e + a)
\end{array}\] biçiminde ayırıp çapraz çarpımı gerçekleştirirsek denklemin orta terimi olan \[2[bc - d(e + a)]x\] ifadesini elde ederiz. O halde \((2)\) nolu denklemin çarpanlara ayrılmış biçimi \[[(b + d)x + c + e + a] \cdot [(b - d)x + c - e - a] = 0\] olur. Bu ifadeden denklemin olası kökleri \[{x_3} = - \frac{{c + e + a}}{{b + d}} \quad {x_4} = - \frac{{c - e - a}}{{b - d}}\] olur. Bu kökler derlenip soruda verilen biçimde gösterilebilir.
Soru
\(a<b\) olmak üzere, şekildeki gibi yarıçapları sırasıyla \(a\) ve \(b\) olan \(O_1\) ve \(O_2\) merkezli çemberler birbirine dıştan teğettir.
Ayrıca ek olarak \(AO_{1}O_{2}\) üçgeninin alanının \[|A{O_1}{O_2}| = \frac{{\sqrt 2 ab\left( {a + b + \sqrt {2ab} } \right)}}{{a + b + 2\sqrt {2ab} }}\] formülü ile bulunabileceğini gösteriniz.
Çözüm
Şekildeki gibi çemberlerin merkezleri ile teğetin değme noktalarını birleştirelim.

\(ADO_1\) dik üçgeninde \[|AD|=\sqrt{x^2+2ax}\] \(AEO_2\) dik üçgeninde \[|AE|=\sqrt{x^2+2bx}\] bulunur.
Şimdi aşağıdaki şekildeki gibi çemberlerin merkezlerini birleştirelim. Ayrıca \(O_1\) den geçen \(d\) ye paralel olan \([FO_1]\) nı çizelim.

\(|FO_{2}|=b-a\) ve \(|O_{1}O_{2}|=a+b\) olduğundan \[|FO_1|=|DE|=\sqrt{4ab}\] bulunur. \(|AD|+|AE|=|DE|\) olduğundan \[\sqrt {{x^2} + 2ax} + \sqrt {{x^2} + 2bx} = \sqrt {4ab} \] olur. Her iki tarafında karesini alırsak
\[\begin{array}{l}
{x^2} + 2ax + {x^2} + 2bx + 2\sqrt {\left( {{x^2} + 2ax} \right) \cdot \left( {{x^2} + 2bx} \right)} = 4ab\\
\Rightarrow {x^2} + 2ax + {x^2} + 2bx - 4ab = - 2\sqrt {\left( {{x^2} + 2ax} \right) \cdot \left( {{x^2} + 2bx} \right)}
\end{array}\] denklemi elde edilir. Bu denklemde \({x^2} + 2ax = m\) ve \({x^2} + 2bx = n\) alırsak, \[m + n - 4ab = - 2\sqrt {mn} \] biçimini alır. Her iki tarafın karesi alırsak
\[\begin{array}{l}
{m^2} + 2mn + {n^2} - 8ab\left( {m + n} \right) + 16{a^2}{b^2} = 4mn\\
\Rightarrow {\left( {m - n} \right)^2} - 8ab\left( {m + n} \right) + 16{a^2}{b^2} = 0
\end{array}\] elde edilir. \(m\) ve \(n\) değerlerini yerini yazıp düzenlersek, \[{x^2}\left( {{a^2} + {b^2} - 6ab} \right) - x\left( {4ab\left( {a + b} \right)} \right) + 4{a^2}{b^2} = 0\] ikinci derece denklemi elde edilir. Bu denklem için diskriminant \[\Delta = 108{a^3}{b^3}\] bulunur. Böylece denklemin kökleri \[{x_{1,2}} = \frac{{2ab\left[ {(a + b) \pm 2\sqrt {2ab} } \right]}}{{{a^2} + {b^2} - 6ab}}\] olur. İfadeyi, pay kısmında yer alan \({(a + b) \pm 2\sqrt {2ab} }\) ifadesinin eşleniği ile genişletirsek \[\frac{{2ab\left[ {(a + b) \pm 2\sqrt {2ab} } \right]}}{{{a^2} + {b^2} - 6ab}} \cdot \frac{{(a + b) \mp 2\sqrt {2ab} }}{{(a + b) \mp 2\sqrt {2ab} }} = \frac{{2ab}}{{(a + b) \mp 2\sqrt {2ab} }}\] elde edilir. O halde bu denklemin kökleri \[{x_{1,2}} = \frac{{2ab}}{{(a + b) \mp 2\sqrt {2ab} }}\] dir. \(x\) değeri bir uzunluk olarak pozitif olacağından, sorumuzda verilen \(x\) için \[x = \frac{{2ab}}{{a + b + 2\sqrt {2ab} }}\] olduğu kanıtlanmış olur.
\(AO_{1}O_{2}\) üçgeninin kenar uzunlukları \(|AO_{1}|=a+x\), \(|AO_{2}|=b+x\) ve \(|O_{1}O_{2}|=a+b\) olduğundan \[u=a+b+x\] olur. Heron alan formülü kullanılırsa \[|A{O_1}{O_2}| = \sqrt {abx\left( {a + b + x} \right)} \] olduğu görülür. Elde ettiğimiz \(x\) değeri yerine yazılıp bu eşitlik düzenlenirse istenilen \[|A{O_1}{O_2}| = \frac{{\sqrt 2 ab\left( {a + b + \sqrt {2ab} } \right)}}{{a + b + 2\sqrt {2ab} }}\] formülü elde edilir.
