Soru
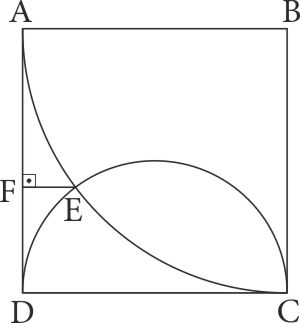
Şekilde \(B\) merkezli çeyrek çember \(ABCD\) karesine içten \(A\) ve \(C\) noktalarında; \([DC]\) çaplı yarım çember ise \(D\) ve \(C\) noktalarında teğettir. \(E\) noktası kesim noktasıdır. \([EF] \bot [AD]\) ve \(|EF|=2\) birim olduğuna göre, \(ABCD\) karesinin alanı kaç birim karedir?
Çözüm 1
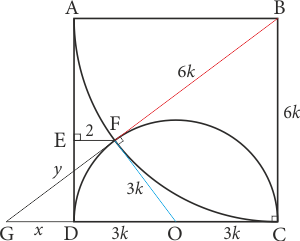
Şekildeki gibi \(BF \cap CD = \{ G\} \) olacak biçimde \([BG]\) ve \([CG]\) çizilsin. \(O\) merkezli yarım çember için \([OF]\) çizilsin. \(|OF|=|OC|=|OD|=3k\) olsun. \(B\) merkezli çeyrek çember için \(|BC|=|BF|=6k\) olur. \([BC]\), \(B\) noktasından \(O\) merkezli yarım çembere çizilen teğet ve \(|BF|=|BC|\) olduğundan \([BF]\) de \(O\) merkezli yarım çembere \(E\) de teğettir. Ek olarak \(OCBF\) dörtgeninin bir deltoid olduğu da görülebilirdi. \([OF]\perp[BG]\) gereği \(BGC \sim OGF\) olur. \(|GD|=x\) ve \(|GF|=y\) dersek benzerlik gereği \[\frac{3k}{{6k}} = \frac{y}{{x + 6k}} = \frac{{x + 3k}}{{y + 6k}}\] olur. Bu eşitlikten \(x = 2k\) ve \(y=4k\) bulunur. Demek ki \(FGO\) ve \(BCG\) üçgenleri birer 3-4-5 üçgenleriymiş.
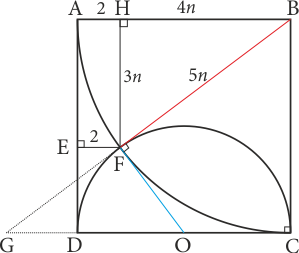
Şekildeki gibi \([FH]\perp[AB]\) çizilirse \(OFG\sim FHB\) olacağından \(FHB\) üçgeni de bir 3-4-5 üçgenidir. \(|HF|=3n\), \(|HB|=4n\) ve \(|BF|=5n\) dersek ve \(|BF|=|BA|\) eşitliği görülürse \[4n+2=5n\] olacağından \(n=2\) ve karenin bir kenar uzunluğu \(10\) birim bulunur. Böylece \[Alan(ABCD)=100\,br^2\] olur.
Çözüm 2 (Erhan Erdoğan)

