3 durumu bu denklemle özetleyebiliriz:
1. Eğer \(<\overrightarrow{N},\overrightarrow{u}>\neq 0\) ise bu eşitlik bize bir tek \(k\) değeri verir. Yani doğru ile düzlem tek bir noktada kesişir.
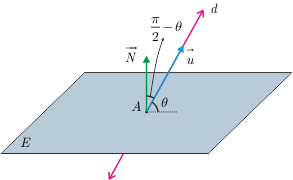
Bu şeklin üç boyutlu Cabri versiyonu için tıklayın!
2. Eğer \(<\overrightarrow{N},\overrightarrow{u}>=0\) ise bu vektörlerin birbirine dik olduğunu yani şekildeki gibi ya doğru düzleme paraleldir ya da düzlemin içindedir.
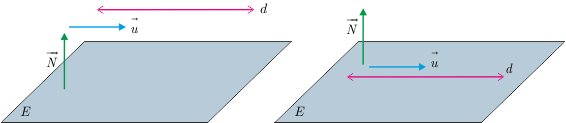
Doğrunun düzleme ait olması için ise \((1)\). eşitlikte payın da sıfır olması gerekir. Yani \(Ax_0+By_0+Cz_0+D=0\) olursa \(k\) herhangi bir gerçek sayı alınabilir çünkü \((1)\). eşitlikte içler dışlar çarpımı yapılırsa \(k\) ne olursa olsun \(k.0=0\) olacaktır.
Örnek 1
\(2x+y-2z-14=0\) düzlemi ile \(\dfrac{x+1}{4}=\dfrac{y-1}{-3}=\dfrac{z}{-5}\) doğrusunun birbirine göre durumunu inceleyiniz.
Çözüm
Doğru denklemini bir \(k\in R\) parametresine bağlı yazalım: $$\begin{matrix}\dfrac{x+1}{4}=\dfrac{y-1}{-3}=\dfrac{z}{-5}=k\\ \Rightarrow x=4k-1\\\Rightarrow y=-3k+1\\\Rightarrow z=-5k\end{matrix}$$ olur. Şimdi düzlem denkleminde bunları yerine yazalım: $$\begin{matrix}2(4k-1)+(-3k+1)-2(-5k)-14=0\\\Rightarrow 15k-15=0\\\Rightarrow k=1 \end{matrix}$$ bulunur. O halde \(k=1\) için \(x=3\), \(y=-2\) ve \(z=-5\) olacak biçimde doğru ile düzlem bir \(A(3,-2,-5)\) noktasında kesişirler.
Tek bir noktada kesişen doğru ve düzlem arasında bir açı oluşacaktır. Şimdi açıklama kısmında verdiğimiz eşitlikten bu açının sinüs değerini bulalım. Düzlemin normal vektörü \(\overrightarrow{N}=(2,1,-2)\) ve doğrunun doğrultu vektörü \(\overrightarrow{u}=(4,-3,-5)\) olduğundan $$sin\theta=\dfrac{2.4+1.(-3)-2.(-5)}{\sqrt{2^2+1^2+2^2}.\sqrt{4^2+3^2+5^2}}=\dfrac{1}{\sqrt{2}}$$ bulunur. O halde doğru ile düzlem arasındaki açının ölçüsü \(\theta=45^{\circ}\) olur.
Aşağıdaki videoda durumu daha detaylı görebilirsiniz.
Örnek 2
\(x-4y+z-1=0\) düzlemi ile \(\dfrac{x+1}{2}=y+3=\dfrac{z-2}{2}\) doğrusunun birbirine göre durumunu inceleyiniz.
Çözüm
Bir \(k\in R\) için doğrunun parametrik denklemini $$\begin{matrix}x=2k-1\\ y=k-3\\z=2k+2\end{matrix}$$ olur. Düzlem denkleminde yerine yazalım $$\begin{matrix}2k-1-4(k-3)+2k+2-1=0\\ \Rightarrow 12=0\end{matrix}$$ elde edilir. Matematiksel olarak doğru olmayan bu ifadenin tek bir anlamı vardır. Doğru ile düzlem kesişmemektedir. Yani doğru düzleme paraleldir. (Düzlemin normal ve doğrunun doğrultu vektörlerinin iç çarpımını da hesaplarsanız \(0\) olduğunu görebilirsiniz, fakat bu durum doğrunun, düzlemin bir doğrusu olup olmadığı hakkında bilgi vermez.)
Örnek 3
\(x-2z=a;\; y=3\) doğrusu \(3x+y-bz+6=0\) düzleminin bir doğrusu olduğuna göre \(a+b\) toplamını bulunuz.
Çözüm
Öncelikle vektörleri bulalım çünkü iç çarpımları \(0\) olmak zorunda. Düzlemin normal vektörü \(\overrightarrow{N}=(3,1,-b)\) ve doğrunun doğrultu vektörü \(\overrightarrow{u}=(2,0,1)\) dir. O halde $$\begin{matrix}<\overrightarrow{N},\overrightarrow{u}>=0\\\\ \Rightarrow 6-b=0 \\\\\Rightarrow b=6\end{matrix}$$ bulunur. Şimdi doğruyu parametrik yazalım fakat diğer sorularda olduğu gibi bir \(k\in R\) ile değil de $$\begin{matrix}z=z\\y=3\\x=2z+a \end{matrix}$$ olarak \(z\) ye bağlı yazalım. Doğru düzlemin bir doğrusu olduğu için bu değerler düzlem denklemini sağlamalıdır: $$\begin{matrix}3(2z+a)+3-6z+6=0\\\\ \Rightarrow 3a+9=0\\\\\Rightarrow a=-3\end{matrix}$$ bulunur. O halde $$a+b=-3+6=3$$ olur.

Şekildeki gibi düzlemler dik kesişmiyorlarsa, aralarında oluşan açılardan biri dar diğeri geniş açı olacaktır. Oluşan dar açıya bu iki düzlem arasındaki açı denir. Şekilde bu açının ölçüsü \(\theta\) olarak verilmiştir. Şimdi bu ölçüyü nasıl hesaplayacağımıza gelelim.

Bu şeklin üç boyutlu Cabri versiyonu için tıklayın!
Şekildeki gibi kesişen düzlemlerin normal vektörlerini çizersek normal vektörleri arasında kalan açı ile düzlemler arasında kalan açının aslında bütünler açılar olduğunu görebiliriz. Bu nedenle düzlemler arasındaki açının ölçüsünü hesaplamak aslında normal vektörleri arasındaki açının ölçüsünü hesaplamakla aynı şeydir. Yani şekle göre
Örnek 1
\(E_1:2x-y+2z-3=0\) düzlemi ile \(E_2: 4x+3y+5z-1=0\) düzlemi arasındaki açının ölçüsü kaç derecedir?
Çözüm
Düzlemler arasındaki açının ölçüsüne \(\theta\) diyelim. \(\overrightarrow{N_1}=(2,-1,2)\) ve \(\overrightarrow{N_2}=(4,3,5)\) olduğundan $$cos\theta=\dfrac{|<\overrightarrow{N_1},\overrightarrow{N_2}>|}{||\overrightarrow{N_1}||||\overrightarrow{N_2}||}=\dfrac{|2.4-1.3+2.5|}{\sqrt{2^2+1^2+2^2}\sqrt{4^2+3^2+5^2}}=\dfrac{1}{\sqrt{2}}$$ olur.
O halde \(\theta=45^{\circ}\) bulunur.
Örnek 2
\(E_1:x-4y+z=3\) düzlemi ile \(E_2:kx+y-5z=3\) düzlemi birbirine dik olduğuna göre \(k\) kaçtır?
Çözüm
Düzlemler birbirine dik olduğuna göre aralarındaki açının ölçüsü \(90^{\circ}\) dir. Yani normal vektörleri de birbirine diktir. Vektörlerde diklik koşulu gereği iç çarpımları \(0\) olmalıdır. İlk düzlem için \(\overrightarrow{N_1}=(1,-4,1)\), ikinci düzlem için \(\overrightarrow{N_2}=(k,1,-5)\) dir. O halde $$<\overrightarrow{N_1},\overrightarrow{N_2}>=0 \Rightarrow 1.k-4.1+1.(-5)=0 \Rightarrow k=9$$ bulunur.
Örnek 3
\(E_1:3x+4y-5z=1\) düzlemi ile \(E_2:-x+ky=10\) düzlemi arasındaki açının ölçüsü \(60^{\circ}\) olduğuna göre \(k\) gerçek sayısının alabileceği değerlerin çarpımı kaçtır?
Çözüm
İlk düzlem için \(\overrightarrow{N_1}=(3,4,-5)\), ikinci düzlem için \(\overrightarrow{N_2}=(-1,k,0)\) dır. O halde $$cos60^{\circ}=\dfrac{|4k-3|}{5\sqrt{2(k^2+1)}}\Rightarrow \dfrac{1}{2}=\dfrac{|4k-3|}{5\sqrt{2(k^2+1)}}$$ olur. Her iki tarafında karesini alıp gerekli düzenlemeyi yaparsak $$7k^2-48k-7=0$$ denklemi elde edilir. Bu denklemden \(k=7\) veya \(k=-\dfrac{1}{7}\) bulunur. Çarpımları da \(-1\) yapar. Elde ettiğimiz denklemin köklerinin gerçek olduğunu tespit ettikten sonra(?)Δ>0 olmalı kökler çarpımı formülünden de bu cevabı bulabilirdik.
Soru
Uzayda \(d_1:2x + z = 4;\; y = 0\) ve \(d_2:y + 2z = 4;\; x = 0\) doğrularının her ikisiyle de dik kesişen doğrunun denklemini bulunuz.
Çözüm
Çözümde geçen detayları anlamak için "Aykırı Doğrular" içeriğini inceleyiniz.
Öncelikle \(d_1\) doğrusunun doğrultu vektörü \(\overrightarrow {{u_1}} = ( - 1,0,2)\) ve sabit noktası \(A(0,0,4)\); \(d_2\) doğrusunun ise doğrultu vektörü \(\overrightarrow {{u_2}} = ( 0,-2,1)\) ve sabit noktası \(A(0,0,2)\) alınabilir. Böylece \(\overrightarrow {AB} = (0,0, - 2)\) olur. Bu üç vektörün belirteceği determinant hesaplanırsa \(0\) dan farklı olduğu görülecektir. Yani bu doğrular aykırı doğrulardır. Bu durumda her ikisiyle kesişen ve her ikisine de dik olan doğru, bu doğruların birbirine en yakın noktalarından geçen doğrudur. \(\overrightarrow N = \overrightarrow {{u_1}} \times \overrightarrow {{u_2}} = (4,1,2)\) vektörünü ve \(\overrightarrow N \times \overrightarrow {{u_2}} = (5, - 4, - 8)\) vektörünü kullanarak \(d_1\) doğrusunun \(d_2\) doğrusuna en yakın noktası \(C = A + k\overrightarrow {{u_1}} \) bulalım. \[ < \overrightarrow {AB} - k\overrightarrow {{u_1}}\quad ,\quad \overrightarrow N \times \overrightarrow {{u_2}} > = 0\] olacağından ifadeler yerine yazılırsa \[k = - \dfrac{{16}}{{21}}\] bulunur. Böylece \[C\left( {\dfrac{{16}}{{21}},0,\dfrac{{52}}{{21}}} \right)\] olur. Ayrıca dikkat edilirse \(\overrightarrow N \) aradığımız doğrunun doğrultu vektörü olacaktır. O halde istenilen doğrunun denklemi gerekli düzenlemelerle : \[\dfrac{{x - 16/21}}{4} = y = \dfrac{{z - 52/21}}{2}\] olarak ifade edilebilir.

