Soru
\(n \geqslant 0\) doğal sayısı için \[{\left( {\begin{array}{*{20}{c}}n \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
2
\end{array}} \right)^2} + \cdot \cdot \cdot + {\left( {\begin{array}{*{20}{c}}
n \\
n
\end{array}} \right)^2} = \left( {\begin{array}{*{20}{c}}
{2n} \\
n
\end{array}} \right)\] eşitliğini kanıtlayınız.
Çözüm 1
En basit biçimiyle \(n\) tane erkek ve \(n\) tane kadın arasından \(n\) adet kişinin kaç farklı biçimde seçileceği sorusunun iki farklı çözümünün getirdiği bir eşitlik olarak düşünülebilir. Toplamda \(2n\) kişi olduğundan, bunlar arasından \(n\) kişi \[\left( {\begin{array}{*{20}{c}}
{2n}\\ n \end{array}} \right)\] farkı biçimde seçilebilir. Öte yandan bu seçimi erkek-bayan seçimleriyle yaparsak;
\(n\) kadın ve \(0\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right)^2}\)
\(n-1\) kadın ve \(1\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right)^2}\)
\(n-2\) kadın ve \(2\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ n-2 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right)^2}\)
.
.
.
\(1\) kadın ve \(n-1\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right)^2}\)
\(0\) kadın ve \(n\) erkek \(\left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right) = {\left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right)^2}\)
olacağından toplamda \[{\left( {\begin{array}{*{20}{c}}
n \\
0
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
1
\end{array}} \right)^2} + {\left( {\begin{array}{*{20}{c}}
n \\
2
\end{array}} \right)^2} + \cdot \cdot \cdot + {\left( {\begin{array}{*{20}{c}}
n \\
n
\end{array}} \right)^2}\] olur. Böylece kanıt tamamlanır.
Çözüm 2
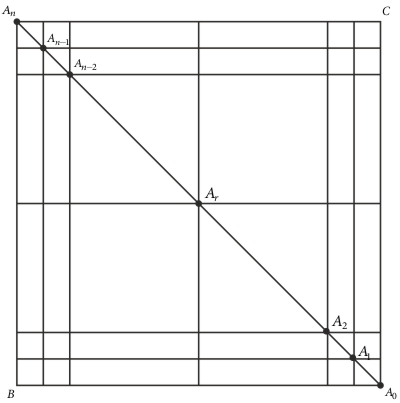
Şekildeki gibi birim karelerden oluşan \(n \times n\) ızgaranın \(B\) köşesinden \(C\) köşesine \(1\) birim sağa ve \(1\) birim yukarı hareket biçimleriyle çizilebilecek farklı yol sayısı \(n\) adet sağ ve \(n\) adet yukarı hareket olduğundan \[\left( {\begin{array}{*{20}{c}}
{2n}\\
n
\end{array}} \right)\] kadardır.
Öte yandan
\(A_0\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_0\) e olan yol sayısı ile \(A_0\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 0 \end{array}} \right)\);
\(A_1\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_1\) e olan yol sayısı ile \(A_1\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right)\);
\(A_2\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_2\) e olan yol sayısı ile \(A_2\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right)\);
.
.
\(A_r\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_r\) e olan yol sayısı ile \(A_r\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ r \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ r \end{array}} \right)\);
.
.
\(A_{n-2}\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_{n-2}\) e olan yol sayısı ile \(A_{n-2}\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ n-2 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n-2 \end{array}} \right)\);
\(A_{n-1}\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_{n-1}\) e olan yol sayısı ile \(A_{n-1}\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n-1 \end{array}} \right)\);
\(A_{n}\) noktasından geçen en kısa yol sayısı, \(B\) den \(A_{n}\) e olan yol sayısı ile \(A_{n}\) den \(C\) ye olan yol sayısının çarpımı olacağından \(\left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} n\\ n \end{array}} \right)\);
olacağından bunların toplamı tüm yol sayısını verecektir. Böylece kanıt tamamlanır.
Çözüm 3
Bir diğer çözüm de \[ {(1 + x)^n} \cdot {(1 + x)^n} = {(1 + x)^{2n}}\] eşitliğinde her iki tarafta da \(x^n\) teriminin katsayısını bulunurak elde edilebilir. Eşitliğin sağında bunun \[\left( {\begin{array}{*{20}{c}}
{2n}\\
n
\end{array}} \right)\] olduğu açıktır. Sol tarafta ise birinci çarpandan gelecek olan \(x^r\) ile ikinci çarpandan gelecek olan \(x^{n-r}\) teriminin katsayıları çarpılacağından \(x^r.x^{n-r}=x^n\) nin katsayısı \[\left( {\begin{array}{*{20}{c}}
n\\
r
\end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}
n\\
{n - r}
\end{array}} \right) = {\left( {\begin{array}{*{20}{c}}
n\\
r
\end{array}} \right)^2}\] olacaktır. \(r=0\) dan \(r=n\) ye kadar bu işlem yapılırsa istenilen eşitlik kanıtlanmış olur.
Catalan Sayıları
Sonlu matematik alanında karşımıza çıkan en belirgin sayı dizilerinden biridir. Bu sayı dizisini öncelikle bir örnekle inceleyelim. (Çalışmanın PDF sürümü konunun bitimindedir.)
Örnek 1
Koordinat düzleminde \((0,0)\) noktasında başlayan iki tür hareket tanımlayalım:
\[S:(x,y) \to (x + 1,y)\] \[Y:(x,y) \to (x,y + 1)\]
S hareketinin 1 birim sağa ve Y hareketinin de 1 birim yukarı olduğunu görüyoruz. Bu hareketleri kullanarak \((0,0)\) noktasından \((5,5)\) noktasına kaç farklı biçimde gidebileceğimizi hesaplamak istersek, 5 adet S ve 5 adet Y kullanmamız gerektiğini görürüz. Bu durumda 5 adet S ve 5 adet Y harfinin her bir farklı sıralaması bir gidiş belirtecektir. O halde toplam gidiş sayısı \(\dfrac{{10!}}{{5! \cdot 5!}} = \left( {\begin{array}{*{20}{c}}
{10}\\5\end{array}} \right)\) kadardır. Şimdi kendimize bir kısıt getirelim ve herhangi bir hareketin \(y = x\) doğrusuna dokunabileceğini ama üstüne çıkamayacağını şart koşalım.
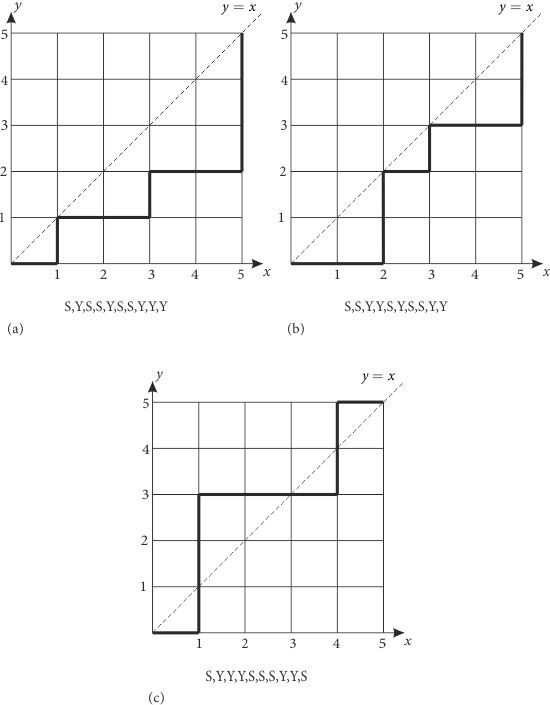
Yukarıdaki şekillerden (a) ve (b) koşulu sağlarken (c) sağlamamaktadır. Koşulumuzda ilk göze çarpan şey herhangi bir gidişin S ile başlayıp Y ile bitmesi gerektiğidir. Ayrıca herhangi bir noktaya kadar yapılan S sayısının Y sayısından az olmayacağı da (a) ve (b) şekillerden gözlemlenebilir. Yani herhangi bir gidişte \(S \ge Y\) dir. (c) şeklinde böyle bir durumun olmadığı da görülebilir. Bu durumların sayısı elde edebilmek için (c) deki gibi koşula uymayan yani \(y = x\) doğrusunun üstünde kalan yolların sayısını elde edip tüm durumdan çıkarabiliriz. (c) deki yolun ne zaman ilk olarak \(S \ge Y\) koşulunu bozduğu yerin 3. hareketten sonra olduğuna dikkate edin. Bunu hareket diziliminde bir çizgi ile gösterirsek
\[S,Y,Y{\rm{ }}|{\rm{ }}Y,S,S,S,Y,Y,S\]
olacaktır. Şimdi bu dizilime aşağıdaki gibi bir dönüşüm uygulayalım.
\[{\mathop{\rm S}\nolimits} ,Y,Y \,\,|\,\, Y,S,S,S,Y,Y,S \Leftrightarrow {\mathop{\rm S}\nolimits} ,Y,Y \,\,|\,\, S,Y,Y,Y,S,S,Y\]
Bu dönüşüm, koşulun bozulduğu ilk andan sonraki hareketleri birbiriyle değiştirmektedir. Yani Y yerine S, S yerine de Y hareketi seçilmektedir. Bu sayede hareket diziliminde 4 adet S ve 6 adet Y olmaktadır. (c) deki bu dönüşüm (d) şeklinde gösterilmektedir. Koşula aykırı bir diğer farklı yolda (e) şeklinde gösterilmektedir. Dönüşümle değişmiş biçimi de (f) de yer almaktadır. Yine 4 adet S ve 6 adet Y hareketi mevcuttur.
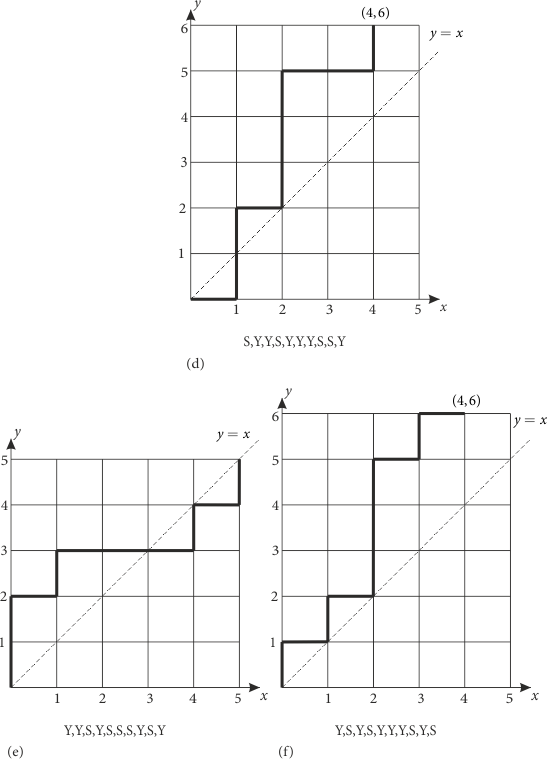
Şimdi 4 S ve 6 Y den oluşan bir hareket dizilimi olarak
\[S,Y,S,S,Y,Y,Y{\rm{ }}|{\rm{ }}Y,Y,S\]
dizilimine bakalım. Y lerin S lerden fazla olduğu ilk hareketten sonrasını çizgi ile ayırmış durumdayız. Bu dizilime dönüşüm uygularsak
\[S,Y,S,S,Y,Y,Y{\rm{ }}|{\rm{ }}S,S,Y\]
eldedilir. Dikkat ederseniz bu 5 S ve 5 Y den oluşan ama koşulumuza aykırı olan bir dizilimdir. Özetle uyguladığımız dönüşümle elde edilen her bir dizilim esasında koşula aykırı bir dizilime denktir. Yani bu biçimde \(\dfrac{{10!}}{{4! \cdot 6!}} = C(10,4)\) hareket dizilimi vardır. O halde koşula uygun
\[C(10,5) - C(10,6) = 42\]
gidiş vardır.
Yukarıdaki örnekle şöyle bir genelleme elde edebiliriz:
\(n \ge 0\) olmak üzere, \(y=x\) doğrusu üzerine çıkmadan \((0,0)\) noktasından \((5,5)\) noktasına \(n\) adet S ve \(n\) adet Y hareketi ile yapılabilecek yol sayısı
\[{b_n} = C(2n,n) - C(2n,n - 1) = \frac{1}{{n + 1}} \cdot C(2n,n), \quad n \ge 1, \quad b_0=1 \]
olur. \({b_0},{b_1},{b_2}, \cdot \cdot \cdot \) sayılarına ismini Belçikalı matematikçi Eugene Charles Catalan ‘dan alan Catalan sayıları denir. Eugene, bu sayıları \({x_1}{x_2}{x_3}...{x_n}\) çarpımını kaç farklı biçimde paranteze alabileceğini hesaplamak için kullanmıştır. Örneğin \({x_1}{x_2}{x_3}{x_4}\) çarpımını \({b_3} = 5\) farklı biçimde paranteze alabiliriz:
\[\left( {\left( {\left( {{x_1}{x_2}} \right){x_3}} \right){x_4}} \right) \quad \left( {\left( {{x_1}\left( {{x_2}{x_3}} \right)} \right){x_4}} \right) \quad \left( {\left( {{x_1}{x_2}} \right)\left( {{x_3}{x_4}} \right)} \right) \quad \left( {{x_1}\left( {\left( {{x_2}{x_3}} \right){x_4}} \right)} \right) \quad \left( {{x_1}\left( {{x_2}\left( {{x_3}{x_4}} \right)} \right)} \right) \]
Örnek 2
Yukarıdaki örnekle özünde aynı ama cümleleri değişik olan aşağıdaki örnekleri inceleyelim.
- 3 adet 1 ve 3 adet – 1 kullanarak elde edilen dizilimlerden \({b_3} = 5\) tanesinde herhangi bir sayıdan önceki sayıların toplamın negatif değildir.
1, 1, 1, -1, -1, -1 1, 1, -1, -1, 1, -1 1, -1, 1, 1, -1, -1
1, 1, -1, 1, -1, -1 1, -1, 1, -1, 1, -1
- 4 adet 1 ve 4 adet 0 kullanılarak elde edilen dizilimlerin \({b_4} = 14\) tanesinde, soldan sağa okunurken, 0 sayısı 1 sayısını geçmez.
10101010 10101100 10110010
10110100 10111000 11001010
11001100 11010010 11010100
11011000 11100010 11100100
11101000 11110000
-
(((ab(c)d)
(((abc
111000
((a(bc))d)
((a(bc
110100
((ab)(cd))
((ab(c
110010
(a((bc)d))
(a((bc
101100
(a(b(cd)))
(a(b(c
101010
Tablonun 1.sütununda abcd çarpımının paranteze alınabilir biçimleri verilmiştir. İlk satırda yer alan (((ab(c)d) biçimini soldan sağa doğru okurken “)” parantezlerini görmezden gelerek 2.sütundaki (((abc dizilimini elde edebiliriz. Benzer biçimde ((a(bc))d) diziliminden ((a(bc elde edilecektir. Şimdi 2.sütundan bir dizilim alıp sonuna “d)” ekleyelim. Örneğin, 3.satırdaki ((ab(c dizilimi ile ((ab(cd) elde edilir. Soldan sağa doğru her bir ikili çarpımı “)” ile kapatırsak ((ab)(cd)) elde edilir. Dikkat ederseniz bu dizilim 1.sütundaki karşılığıdır.
3.sütunun ne olduğu açık bir biçimde görülmektedir. “(“ sembollerini 1; a, b ve c harflerini de 0 sembolize etmektedir. O halde 1.sütunda yer alan her bir dizilime karşılık, 3 adet 1 ve 3 adet 0 içeren ve soldan sağa okunurken 0 sayısının 1 sayısından fazla olmadığı bir sayı dizisi karşılık gelmektedir. Bunların sayısının da \({b_3} = 5\) olduğu görülmektedir. O halde, genel olarak \({x_1}{x_2} \cdot \cdot \cdot {x_n}\) çarpımını \({b_{n - 1}}\) farklı biçimde paranteze alabilir.
- Şimdi, 1,2,3,4,5 ve 6 sayılarını 2 satır ve 3 sütundan oluşan bir tabloda (1) her bir satırda sayılar soldan sağa doğru okunurken küçükten büyüğe doğru dizili, (2) herhangi bir sütunda küçük sayı üstte olacak biçimde dizmeye çalışalım. Örneğin,
1
2
4
3
5
6
Şimdi ilk satırda yer alan sayıları 1 ile ikinci satırda yer alan sayıları da 0 ile sembolize ederek tablodaki sayıların sırasına göre bir dizilim yaparsak \(123456 \leftrightarrow 110100\) elde ederiz. Şimdi tam tersi 0 sayısının 1 sayısını soldan sağa geçmediği rastgele bir dizilimi ele alıp tablo oluşturalım. Örneğin, \(101100 \leftrightarrow 123456\) ile
1
3
4
2
5
6
elde edilir ki istenilen koşullara uygun bir tablomuz olur. O halde bu sorunun cevabı da \({b_3} = 5\) olacaktır.
Kaynakça: Ralph P. Grimaldi, Discrete and Combinatorial Mathematics, 5th Edition
Soru
Ege, Irmak ve Çınar aralarında anlaşıp bir alışveriş merkezinde saat 12:00 ile 13:00 arasında buluşacaklardır. İlk gelen, herhangi biri 10 dakika içinde gelmezse, alışveriş merkezini terkedecektir. Eğer 10 dakika içinde biri gelirse, ikisi birlikte üçüncü kişiyi en fazla 10 dakika bekleyecektir.
Buna göre, Ege, Irmak ve Çınar'ın buluşma olasılığını hesaplayınız.
Çözüm
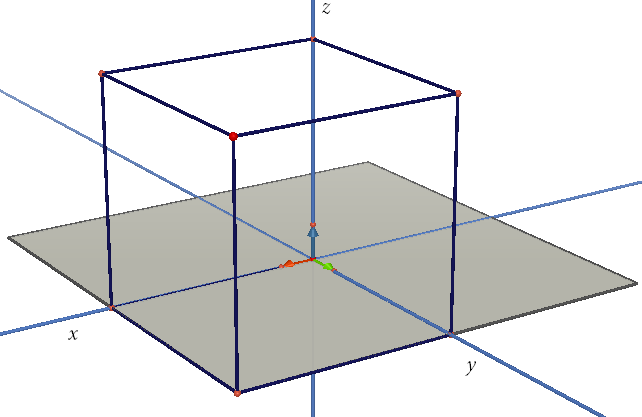
Öncelikle zaman dilimini bir reel aralığa indirgeyelim. 12:00 ı başlangıç ve 13:00 ı bitiş noktası seçerek [0,60] reel aralığını kullanacağız. Sırasıyla Ege, Irmak ve Çınar'ın gelme sürelerine \(x\), \(y\) ve \(z\) diyelim. Örneğin Çınar saat 12:32 de gelmişse \(z=32\) olacaktır. Böylece \((x,y,z)\) sıralı üçlüleri elde ederiz. Ayrıca \(0\le x \le 60\), \(0\le y \le 60\) ve \(0\le z \le 60\) olduğuna dikkat edin. Bu durumda bu sıralı \((x,y,z)\) üçlüleri aşağıdaki şekilde görüleceği üzere \(R^3\) te bir ayrıtı 60 birim olan bir küp belirteceklerdir. Böylece örnek uzayımız bu küpün hacmi olacaktır.
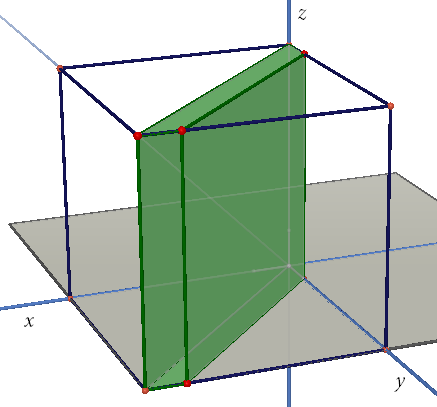
 Şimdi ilk gelenin Ege, sonra Irmak ve en son Çınar olduğunu varsayalım. Bu durumda buluşmanın gerçekleşebilmesi için Irmak'ın Ege'den sonra en çok 10 dakika içinde gelmiş olması gerekir. Yani \[x \le y \le x + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=x\) ve \(y=x+10\) düzlemleri arasında kalan bölge olacaktır.
Şimdi ilk gelenin Ege, sonra Irmak ve en son Çınar olduğunu varsayalım. Bu durumda buluşmanın gerçekleşebilmesi için Irmak'ın Ege'den sonra en çok 10 dakika içinde gelmiş olması gerekir. Yani \[x \le y \le x + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=x\) ve \(y=x+10\) düzlemleri arasında kalan bölge olacaktır.
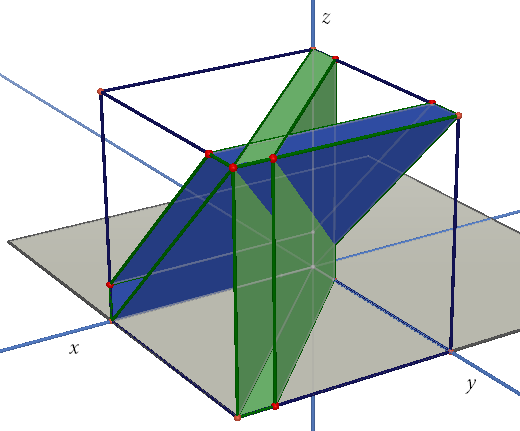
 Ayrıca Çınar'ında Irmak'tan en çok 10 dakika sonra gelmesi gerekeceğinden \[y \le z \le y + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=z\) ve \(z=y+10\) düzlemleri arasında kalan bölge olacaktır.
Ayrıca Çınar'ında Irmak'tan en çok 10 dakika sonra gelmesi gerekeceğinden \[y \le z \le y + 10\] olmalıdır. Aşağıdaki şekilde görüleceği üzere, \(R^3\) te bu eşitsizlik \(y=z\) ve \(z=y+10\) düzlemleri arasında kalan bölge olacaktır.
 O halde buluşmanın bu şartlarda gerçekleşmesini gösteren bölge bu dört düzlemin ifade ettiği aşağıdaki videodaki gibi olacaktır.
O halde buluşmanın bu şartlarda gerçekleşmesini gösteren bölge bu dört düzlemin ifade ettiği aşağıdaki videodaki gibi olacaktır.
Oluşan bu cismin hacmini bulabilmek için cismi aşağıdaki videoda gösterildiği üzere \(y=10\) ve \(y=50\) düzlemleriye kesersek iki düzlem arasında kalan cisim kare eğik prizma olurken, uç noktalarda kalan parçalar kare eğik yarım prizmalar olacaktır.
Daha detaylı incelemek gerekirse, öncelikle aşağıdaki şekilde görülen yarım eğik kare prizmaya bakalım.
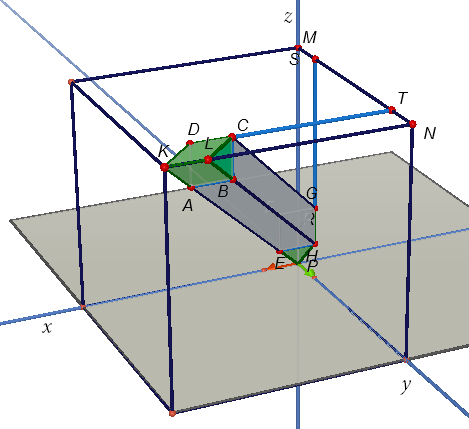 Prizmanın tabanı bir kenarı \(10\) birim olan \(ABCD\) karesidir. Yüksekliği ise \(|TN|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. Benzer biçimde aşağıdaki şekilde görüleceği üzere,diğer yarım eğik kare prizmanın
Prizmanın tabanı bir kenarı \(10\) birim olan \(ABCD\) karesidir. Yüksekliği ise \(|TN|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. Benzer biçimde aşağıdaki şekilde görüleceği üzere,diğer yarım eğik kare prizmanın
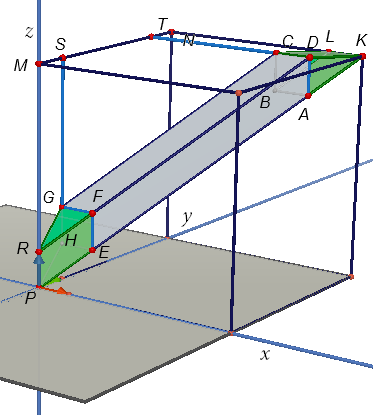 tabanı bir kenarı \(10\) birim olan \(GFEH\) karesidir. Yüksekliği ise \(|MS|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. O halde bu iki yarım prizmanın hacimleri toplamı \[{10^3}\] tür.
tabanı bir kenarı \(10\) birim olan \(GFEH\) karesidir. Yüksekliği ise \(|MS|=10\) birimdir. Bu nedenle hacmi \(\dfrac{1}{2} \cdot {10^2} \cdot 10\) olur. O halde bu iki yarım prizmanın hacimleri toplamı \[{10^3}\] tür.
Tabanları \(GFEH\) ve \(ABCD\) olan ve arada kalan eğik prizmanın yüksekliği de yukarıdaki şekillerde görüleceği üzere \(|TS|=40\) birim olacağından, hacmi \({10^2} \cdot 40\) olur. Böylece cismin toplam hacmi \[{10^2} \cdot 50\] olacaktır.
Daha geniş algı için aşağıdaki videoyu izleyebilirsiniz.
Bu cismi elde ederken gelme sırasını Ege, Irmak ve Çınar biçiminde kabul etmiştik. Oysa biliyoruz ki toplamda \(3! = 6\) farklı sıralama ile buluşma gerçekleşebilir. Bu da demektir ki bu cisimden \(6\) adet vardır. Aşağıdaki şekilde tüm cisimlerin videosunu gözlemleyebilirsiniz.
O halde istenilen olasılık \[P = \frac{{6 \cdot {{10}^2} \cdot 50}}{{{{60}^3}}} = \frac{5}{{36}}\] olarak bulunur.

