Soru
\[y = a{x^2} + bx + c\] parabolünün dik kesişen teğetlerinin kesim noktalarının geometrik yerinin \[y = - \dfrac{{\Delta + 1}}{{4a}}\] olduğunu gösteriniz.
Çözüm
Verilen parabolün dik kesişine teğetlerinden rastgele ikisinin kesiştiği nokta \(P(x_0,y_0)\) olsun. Bu teğetlerin eğimlerine sırasıyla \({m_1}\) ve \({m_2}\) diyelim. Bu durumda teğetlerin denklemleri sırasıyla \[y = {m_1}(x - {x_0}) + {y_0}\] ve \[y = {m_2}(x - {x_0}) + {y_0}\] olacaktır. Biz eğimlere genel olarak \(m\) diyerek her iki teğeti de kapsayan \[y = m(x - {x_0}) + {y_0}\] denklemini yazalım. Teğetler ile parabolün kesim noktası tek olduğundan, bu denklem ile parabolün denkleminin ortak çözümünden elde edilecek olan 2. dereceden bir bilinmeyenli denklemin tek kökü yani diskriminantı 0 a eşit olmalıdır: \[\begin{array}{*{20}{c}} {m(x - {x_0}) + {y_0} = a{x^2} + bx + c}\\ { \Rightarrow a{x^2} + x(b - m) + c + m{x_0} - {y_0} = 0} \end{array}\] olacağından \[\begin{array}{l} \Delta = {(b - m)^2} - 4a(c + m{x_0} - {y_0}) = 0\\ \Rightarrow {m^2} + m( - 2b - 4a{x_0}) + {b^2} - 4ac + 4a{y_0} = 0 \end{array}\] elde edilir. Elde edilen \(m\) ye bağlı bu 2.dereceden denklemden elde edilecek olan \({m_1}\) ve \({m_2}\) kökleri teğetlerin eğimleri olacaktır. Fakat biliyoruz ki teğetler dik kesişmektedir. O halde \[{m_1} \cdot {m_2} = - 1\] dir. Bu durumda elde ettiğimiz \(m\) ye bağlı bu 2.dereceden denklemde \[\begin{array}{l} \dfrac{c}{a} = - 1\\ \Rightarrow \dfrac{{{b^2} - 4ac + 4a{y_0}}}{1} = - 1\\ \Rightarrow \Delta + 4a{y_0} = - 1\\ \Rightarrow {y_0} = - \dfrac{{\Delta + 1}}{{4a}} \end{array}\] elde edilir. O halde dik kesişen teğetlerin kesim noktasının ordinatı daima bu değere eşittir. Demek ki bu noktalar \[y = - \dfrac{{\Delta + 1}}{{4a}}\] doğrusu üzerindedir.
Böylece ispat tamamlanmış olur.
Şimdi, parabolün denklemi genel konik denklemine dönüştürelim. \[\begin{array}{l}
y = a\left[ {{x^2} + \dfrac{b}{a}x + \dfrac{c}{a}} \right]\\ \Rightarrow y = a\left[ {{x^2} + \dfrac{b}{a}x + \dfrac{{{b^2}}}{{4{a^2}}} - \dfrac{{{b^2}}}{{4{a^2}}} + \dfrac{c}{a}} \right]\\ \Rightarrow \dfrac{1}{a}y = \left[ {{{\left( {x + \dfrac{b}{{2a}}} \right)}^2} - \dfrac{{{b^2} - 4ac}}{{4{a^2}}}} \right]\\ \Rightarrow \dfrac{1}{a}y = {\left( {x + \dfrac{b}{{2a}}} \right)^2} - \dfrac{\Delta }{{4{a^2}}}\\ \Rightarrow \dfrac{1}{a}\left( {y + \dfrac{\Delta }{{4a}}} \right) = {\left( {x + \dfrac{b}{{2a}}} \right)^2} \end{array}\] elde edilir. Böylece merkezi \[M\left( { - \dfrac{b}{{2a}}, - \dfrac{\Delta }{{4a}}} \right)\] ve parametresi \[p = \dfrac{1}{{2a}}\] olan ötelenmiş parabol denklemi elde ederiz. Öteleme vektörü \[\overrightarrow u = \left( {-\dfrac{b}{{2a}},-\dfrac{\Delta }{{4a}}} \right)\] olduğundan parabolün doğrultmanı \[\begin{array}{l}
y = - \dfrac{p}{2} - \dfrac{\Delta }{{4a}}\\ \Rightarrow y = - \dfrac{1}{{4a}} - \dfrac{\Delta }{{4a}} = - \dfrac{{\Delta + 1}}{{4a}} \end{array}\] olur. Demek ki parabolün dik kesişen teğetlerinin kesim noktalarının geometrik yeri aynı zamanda parabolün doğrultmanıdır.
Soru
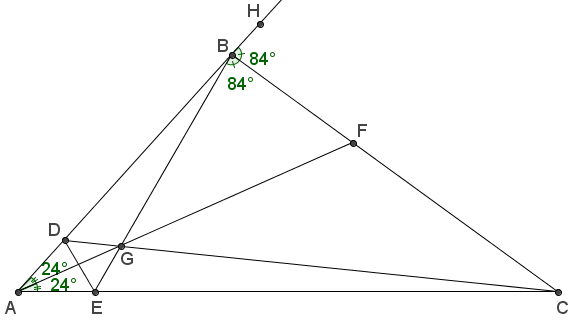
Şekildeki \(ABC\) üçgeninde, \([CD] \cap [BE] \cap [AF] = \left\{ G \right\}\), \(m(\widehat {BAF}) = m(\widehat {CAF}) = {24^ \circ }\), \(m(\widehat {CBE}) = m(\widehat {CBH}) = {84^ \circ }\) ve \(A\), \(B\) , \(H\) doğrusal olduğuna göre, \[m(\widehat {CDE})\] kaç derecedir?
Çözüm 1 - Temel GÖKÇE
Buradan \[|CE| = \frac{{|CA|.|BE|}}{{|BA|}}\] elde edilir. \(\triangle ABC\) ninde \([AF]\) iç açıortay olduğundan \(\dfrac{{|CA|}}{{|AB|}} = \dfrac{{|CF|}}{{|BF|}}\) dir.
Buradan \[|BF| = \frac{{|AB|.|CF|}}{{|CA|}}\] olur.
\(\triangle ABC\) ninde Seva teoremi uygulanırsa \[\frac{{|CE|}}{{|EA|}}.\frac{{|AD|}}{{|DB|}}.\frac{{|BF|}}{{|FC|}} = 1\] olur. Yukarıda bulduğumuz eşitlikleri yerine yazarsak \[\frac{{|CA|.|BE|}}{{|BA|.|EA|}}.\frac{{|AD|}}{{|DB|}}.\frac{{|AB|.|CF|}}{{|FC|.|CA|}} = 1\] olur. Sadeleştirmeler yapılırsa \[\frac{{|BE|}}{{|EA|}} = \frac{{|DB|}}{{|AD|}}\] elde edilir. O halde \([ED]\), \(\triangle AEB\) nin iç açıortayıdır. Bu durumda \(m(\widehat {AEG}) = {120^ \circ }\) olduğundan \[m(\widehat {AED}) = m(\widehat {DEB}) = m(\widehat {BEC}) = {60^ \circ }\] olur.
Demek ki \([EB]\) de \(\triangle ADE\) nin dış açıortayıdır. Bu üçgende \([AF]\) de iç açıortay olduğundan \([DC]\) de dış açıortay olur. Böylece \[m(\widehat {CDE}) = {54^ \circ }\] bulunur.
Çözüm 2 - Süleyman SÖYLER
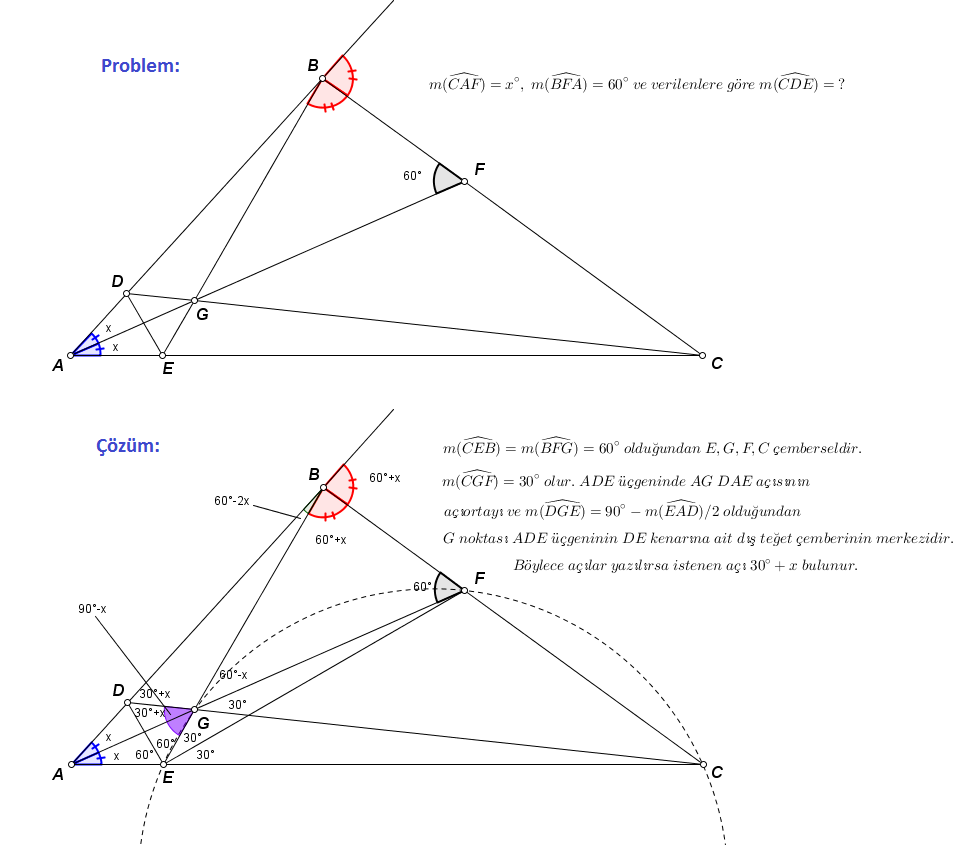
Çözümler için Temel GÖKÇE ve Süleyman SÖYLER öğretmenlerime teşekkür ediyorum.
Sorunun özünde \(\triangle AEB\) nin \(A\) ve \(E\) köşelerinden çıkan iç açıortaylarının sırasıyla kenarları kestiği noktalar olan \(G\) ve \(D\) ile, \(B\) köşesinden çıkan dış açıortayının \(AE\) yi kestiği nokta olan \(C\) nin daima doğrusal olması yatıyor. Bunun ispatı, 1. çözümde geçen yöntemle yapılabilir.
Soru
\(A = \{ 1,2,3,...,n\} \) kümesi verilsin.
- \(A\) kümesinin boş kümeden farklı herhangi bir alt kümesi \(A_i\) olsun. \(A_i\) kümesinin elemanlarının çarpımı da \(X_i\) olsun. Buna göre, tüm \(X_i\) değerlerinin toplamını \(n\) cinsinden ifade ediniz.
- \(A\) kümesinin boş kümeden farklı ve eleman sayısı çift olan herhangi bir alt kümesi \(B_i\) olsun. Bu kümenin elemanlarının çarpımı da \(Y_i\) olsun. Buna göre, tüm \(Y_i\) değerlerinin toplamını \(n\) cinsinden ifade ediniz.
- \(A\) kümesinin boş kümeden farklı ve eleman sayısı tek olan herhangi bir alt kümesi \(C_i\) olsun. Bu kümenin elemanlarının çarpımı da \(Z_i\) olsun. Buna göre, tüm \(Z_i\) değerlerinin toplamını \(n\) cinsinden ifade ediniz
Çözüm
\(n\) çift ise \[\begin{array}{l} f( - 1) = ( - 2)( - 3) ... ( - 1 - n) = 1 - {b_1} + {b_2} - {b_3} + ... + {b_n}\\ \Rightarrow - {b_1} + {b_2} - {b_3} + ... + {b_n} = (n + 1)! - 1 \end{array}\] olurken
\(n\) tek ise \[\begin{array}{l} f( - 1) = ( - 2)( - 3) ... ( - 1 - n) = - 1 + {b_1} - {b_2} + {b_3} - ... - {b_n}\\ \Rightarrow - {b_1} + {b_2} - {b_3} + ... + {b_n} = (n + 1)! - 1 \end{array}\] olmaktadır. (İkinci durumda \(n\) tek olduğundan \(( - 2)( - 3) ... ( - 1 - n) = - (n + 1)!\) olduğuna dikkat ediniz.)
O halde her iki durumda da köklerin birbirleriyle farklı çarpımları toplamının \((n+1)!-1\) olduğunu görüyoruz. Bu, \(A = \{ 1,2,3,...,n\} \) kümesi için ilk soruda aradığımız cevaptan başka birşey değildir. Çünkü \(A\) kümesinin belli bir sayıda eleman (örneğin 2 eleman) ieçeren alt kümelerin elemanlarının çarpımları toplamı ile yazdığımız \(f\) fonksiyonun köklerinin belli bir miktarda (örneğin ikişerli biçimde) çarpımının toplamı aynıdır. O halde ilk soru için cevabımız \[(n + 1)! - 1\] dir.
Şimdi ikinci sorunun çözümünü verelim. Dikkat ederseniz yazdığımız \(f\) fonksiyonu için \(f(1) = 0\) dır. Öte yandan \[f(1) = 1 + {b_1} + {b_2} + ... + {b_n}\] dir. Ayrıca \(n\) çift için \[f( - 1) = 1 - {b_1} + {b_2} - {b_3} + ... + {b_n}=(n+1)!\] olduğunu yukarıda ifade etmiştik. \(f(1)\) ve \(f(-1)\) değerlerini toplarsak \[2(1 + {b_2} + {b_4} + ... + {b_n}) = (n + 1)!\] bulunur. Demek ki \[{b_2} + {b_4} + ... + {b_n} = \frac{{(n + 1)!}}{2} - 1\] dir. (\(n\) tek için de aynı durumun geçerli olacağını siz gösteriniz.) O halde \(A\) kümesinin boş kümeden farklı çift sayıda eleman içeren kümelerindeki elemanların çarpımları toplamı \[\frac{{(n + 1)!}}{2} - 1\] olur.
Son sorumuzada \(f(1)\) ve \(f(-1)\) farkından cevap verebiliriz, ama en kısa çözümümüz tabiki tüm durumdan çift olanların durumunu çıkarmak olacaktır. Yani \(A\) kümesinin boş kümeden farklı tek sayıda eleman içeren kümelerindeki elemanların çarpımları toplamı \[(n + 1)! - 1 - \left( {\frac{{(n + 1)!}}{2} - 1} \right) = \frac{{(n + 1)!}}{2}\] bulunur.

