2012 LYS Geometri Sorularının Çözümleri
Soru
Bir doğru parçası eş zamanlı olarak 4 parçaya ayrılıyor. Bu parçaların bir dışbükey dörtgen belirtme olasılığı kaçtır?
Çözüm
Sorunun çözümüne geçmeden önce "aynı anda 3 parçaya bölünen doğru parçasının bu parçalarının üçgen belirtme, dar açılı üçgen belirtme ve geniş açılı üçgen belirtme olasığı" üzerine eski çalışmamı izlemenizi tavsiye ederim.
Öncelikle şunu kanıtlayalım:
Kanıt:
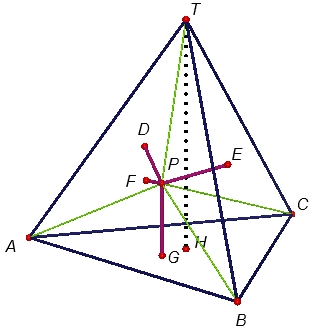
Şekildeki gibi \((T,ABC)\) düzgün dörtyüzlüsü içinde bir P noktası alınsın ve sırasıyla yüzeylerine çizilen dikmeleri \([PD]\), \([PE]\), \([PF]\) ve \([PG]\) olsun. Dörtyüzlünün yüksekliği \([TH]\) ve \([PA]\), \([PB]\), \([PC]\), \([PT]\) çizilsin. Bu durumda düzgün dörtyüzlüyü oluşturan \((P,ATB)\), \((P,ATC)\), \((P,BTC)\) ve \((P,ABC)\) piramitleri elde edilmiş olur. Bu piramitlerin taban alanları, dörtyüzlünün yüzeyleri olduğundan, eşittirler. Dörtyüzlünün bir yüzeyinin alanına \(S\) dersek, piramitlerin hacimleri sırasıyla \(\dfrac{1}{3} \cdot S \cdot |PF|\), \(\dfrac{1}{3} \cdot S \cdot |PD|\), \(\dfrac{1}{3} \cdot S \cdot |PE|\) ve \(\dfrac{1}{3} \cdot S \cdot |PG|\) dir. O halde bunların toplamı dörtyüzlünün hacmine eşit olmalıdır: \[\begin{array}{l}
\frac{1}{3} \cdot S \cdot |TH| = \frac{1}{3} \cdot S \cdot \left[ {|PF| + |PD| + |PE| + |PG|} \right]\\
\\
\Rightarrow |TH| = |PF| + |PD| + |PE| + |PG|
\end{array}\] olur.
Videoyu izleyerek görsel destek alabilirsiniz.
Bu kanıttan sonra belki tahmin etmişsinizdir; soruda verilen doğru parçası dörtyüzlünün yüksekliği \([TH]\) ve ayrılan dört parça \([PD]\), \([PE]\), \([PF]\) ve \([PG]\) olacak biçimde soruyu çözeceğiz. Parçaların dörtgen oluşturabilmesi için her birinin uzunluğu \([TH]\) ın yarısından küçük olmalıdır. Aksi halde dörtgen oluşmayacağı aşikardır. Bu şartın sağlanması için \(P\) noktasının
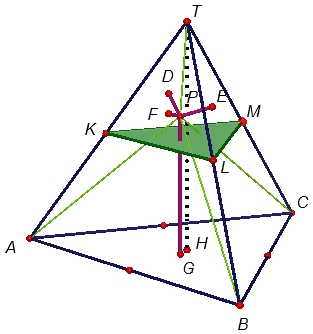
şekildeki gibi, taban köşeleri \((T,ABC)\) nin yan ayrıtlarının orta noktaları olan, \((T,KLM)\) düzgün dörtyüzlüsü içinde yer almaması gerekir. Çünkü bu durumda \[|PG| > \dfrac{{|TH|}}{2}\] olacaktır. Benzer biçimde \(P\) nin bulunmaması gereken bölgeler aşağıdaki şekilde verilmiştir.
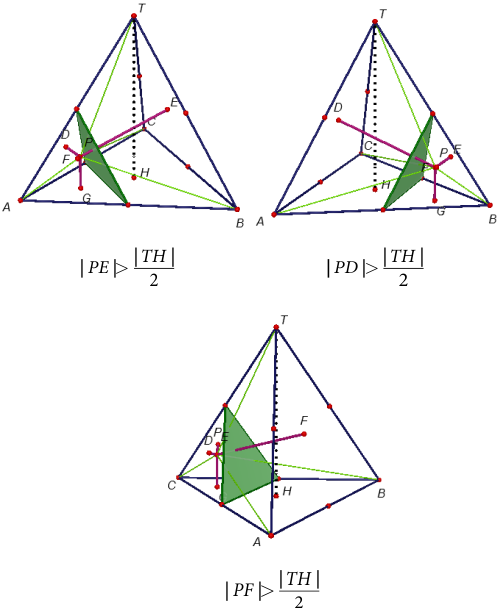
Benzerlik gereği düzgün dörtyüzlünün hacminin bunlardan birinin hacmine oranı \[{\left( {\frac{1}{2}} \right)^3} = \frac{1}{8}\] dir. O halde \[{V_{(T,ABC)}} = 8V\] dersek; istenmeyen bölgenin hacmi \[{V_{istenmeyen}} = 4V\] olacaktır. Böylece istenilen olasılık \[P = 1 - \frac{{4V}}{{8V}} = \frac{1}{2}\] bulunur.
Videoda \(P\) noktasının bulunması gereken bölgenin asında düzgün dörtyüzlünün orta sekizyüzlüsü olduğunu görebilirsiniz.
Esasında bu soruyu 5 parça için sorsaydık, her ne kadar 4.boyuta geçiyor olsak ve bunu çizemesekte, istenmeyen (hiper)bölge sayısının 5 ve benzerlik oranının \({\left( {\dfrac{1}{2}} \right)^4} = \dfrac{1}{{16}}\) olacağını sezebiliriz. Yani 5 gen oluşturma olasılığı \[P = 1 - \frac{{5V}}{{16V}} = \frac{{11}}{{16}}\] olurdu.
Genel olarak eş zamanlı olarak n parçaya bölünen bir doğru parçasının, bu parçalarının bir n-gen belirtme olasılığı \[1 - \frac{n}{{{2^{n - 1}}}}\] dir.
Bu konuyla ilgili değerli meslektaşım Lokman GÖKÇE'nin hazırladığı "Geometrik Olasılık" başlığı Geomania sitesinde ziyaret edilebilir.
Soru
\[{d_1}:2x = y = z\] \[{d_2}:x = 2y = z\] doğrularına teğet, yarıçapı \(\dfrac{3\sqrt{5}}{2}\) birim olan ve merkezi \(x-2y=0\) düzleminde bulunan kürelerin denklemlerini bulunuz.
Çözüm
Öncelikle \({d_1}\) doğrusunun doğrultu vektörünün \(\overrightarrow {{u_1}} = (1,2,2)\) ve \({d_2}\) doğrusunun doğrultu vektörünün \(\overrightarrow {{u_2}} = (2,1,2)\) olduğunu görelim. Ayrıca doğruların \(O(0,0,0)\) noktasında kesiştiğini görelim. İstenilen kürelerin merkezi \(x = 2y\) düzleminde olduğundan bu noktaları \(P(2y,y,z)\) biçiminde gösterebiliriz. Küreler doğrulara teğet olduğundan, merkezin doğrulara olan uzaklıkları eşit ve yarıçap kadar olmalıdır. (Noktanın doğruya uzaklığı için tıklayınız!) Yani \[\frac{{||\overrightarrow {OP} \times \overrightarrow {{u_1}} |{\kern 1pt} |}}{{||\overrightarrow {{u_1}} ||}} = \frac{{||\overrightarrow {OP} \times \overrightarrow {{u_2}} |{\kern 1pt} |}}{{||\overrightarrow {{u_2}} ||}} = \frac{3\sqrt 5}{2} \] olmalıdır. Bu eşitlikte \(||\overrightarrow {{u_1}} || = ||\overrightarrow {{u_2}} || = 3\) olduğuna dikkat edersek \[||\overrightarrow {OP} \times \overrightarrow {{u_1}} |{\kern 1pt} | = ||\overrightarrow {OP} \times \overrightarrow {{u_2}} |{\kern 1pt} |\] eşitliğini çözmeye çalışalım. \[\overrightarrow {OP} \times \overrightarrow {{u_1}} = \left| {\begin{array}{*{20}{c}}
{\overrightarrow {{e_1}} }&{\overrightarrow {{e_2}} }&{\overrightarrow {{e_3}} }\\
{2y}&y&z\\
1&2&2
\end{array}} \right| = (2y - 2z\,,\,z - 4y\,,\,3y)\] ve \[\overrightarrow {OP} \times \overrightarrow {{u_2}} = \left| {\begin{array}{*{20}{c}}
{\overrightarrow {{e_1}} }&{\overrightarrow {{e_2}} }&{\overrightarrow {{e_3}} }\\
{2y}&y&z\\
2&1&2
\end{array}} \right| = (2y - z\,,\,2z - 4y\,,\,0)\] olur. Uzunluklarını eşitlersek \[y \cdot (9y + 4z) = 0\] denklemi elde edilir. Böylece \(y = 0\) için kürelerden birinin merkezi \[P(0,0,z)\] \(9y = -4z\) için ise bir \(k\) parametresine bağlı olarak diğer kürenin merkezi \[P(8k,4k,-9k)\] olacaktır. \(P(0,0,z)\) için \[\overrightarrow {OP} \times \overrightarrow {{u_1}} = ( - 2z,z,0)\] olacağından \[\frac{{||\overrightarrow {OP} \times \overrightarrow {{u_1}} ||}}{{||\overrightarrow {{u_1}} ||}} = \frac{{3\sqrt 5 }}{2}\] eşitliğinde yerine yazarsak \(|z|=\dfrac{9}{2}\) olur. Böylece bu şartlarda merkezleri sırasıyla \[P\left( {0\,,0\,,\,\frac{9}{2}} \right)\] ve \[P\left( {0\,,0\,,\,-\frac{9}{2}} \right)\] olan iki küre elde edilir. Bu kürelerin denklemleri \[{x^2} + {y^2} + {\left( {z - \frac{9}{2}} \right)^2} = \frac{{45}}{4}\] ve \[{x^2} + {y^2} + {\left( {z + \frac{9}{2}} \right)^2} = \frac{{45}}{4}\] olacaktır. Öte yandan \(P(8k,4k,-9k)\) için \[\overrightarrow {OP} \times \overrightarrow {{u_1}} = (26k\,, - 25k\,,\,12k)\] olacağından \[\frac{{||\overrightarrow {OP} \times \overrightarrow {{u_1}} ||}}{{||\overrightarrow {{u_1}} ||}} = \frac{{3\sqrt 5 }}{2}\] eşitliğinde yerine yazılırsa \[|k| = \frac{9}{{34}}\] bulunur. Böylece tekrar iki farklı merkez elde ederiz: \[P\left( {\frac{{36}}{{17}}\,,\,\frac{{18}}{{17}}\,,\,\frac{{-81}}{{34}}} \right)\] ve \[P\left( {-\frac{{36}}{{17}}\,,\,-\frac{{18}}{{17}}\,,\,\frac{{81}}{{34}}} \right)\] bulunur. Kürelerin denklemleri de \[{\left( {x - \frac{{36}}{{17}}} \right)^2} + {\left( {y - \frac{{18}}{{17}}} \right)^2} + {\left( {z + \frac{{81}}{{34}}} \right)^2} = \frac{{45}}{4}\] ve \[{\left( {x + \frac{{36}}{{17}}} \right)^2} + {\left( {y + \frac{{18}}{{17}}} \right)^2} + {\left( {z - \frac{{81}}{{34}}} \right)^2} = \frac{{45}}{4}\] olur. Özetle verilen şartlara uygun 4 farklı küre vardır.

