Soru
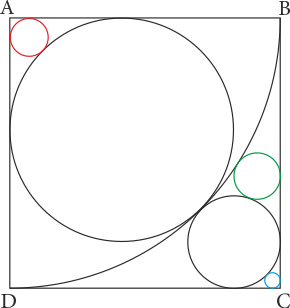 Şekildeki ABCD karesinde A merkezli çeyrek çember ile 5 çember verilmiştir. Çemberler şekildeki gibi kareye ve birbirine teğettir. Mavi ve kırmızı çemberlerlerin yarıçapları toplamı √2 olduğuna göre, yeşil çemberin yarıçapı kaç birimdir?
Şekildeki ABCD karesinde A merkezli çeyrek çember ile 5 çember verilmiştir. Çemberler şekildeki gibi kareye ve birbirine teğettir. Mavi ve kırmızı çemberlerlerin yarıçapları toplamı √2 olduğuna göre, yeşil çemberin yarıçapı kaç birimdir?
Çözüm
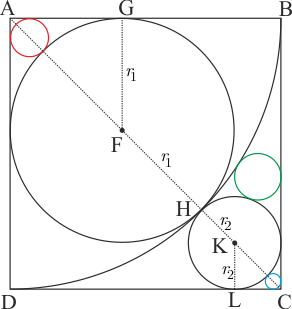
AGF üçgeninde |AF|=r1√2 dir. KLC üçgeninde |KC|=r2√2 dir. Bu durumda |AC|=(r1+r2)(√2+1) olur. |AH|=r1(√2+1) karenin bir kenarına eşit olduğundan |AC|=√2|AH| olur. O halde (r1+r2)(√2+1)=√2r1(√2+1) eşitliğinden r2r1=√2−1(...1) bulunur.
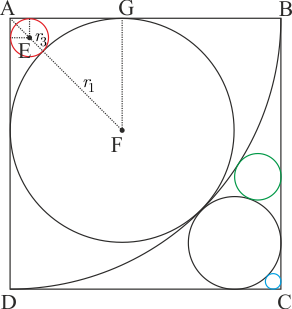
Şekildeki gibi kırmızı çemberin yarıçapına r3 dersek ve merkeziyle karenin kenarlarına dik çizip gerekli işlemleri yaparsak AF|=|AE|+|EF|=r3√2+r3+r1 olurken AGF üçgeninde |AF|=r1√2 olduğundan r3√2+r3+r1=r1√2 olur. Bu eşitlikten r3=r1.√2−1√2+1(...2) elde edilir. Benzer biçimde mavi çemberin yarıçapına r4 dersek, ilk şekilde |KC|=r2+r4+r4√2 bulunur. Ayrıca |KC|=r2√2 olduğundan r4=r2.√2−1√2+1(...3) elde edilir. Elde ettiğimiz son iki eşitliği taraf tarafa oranlarsak r4r3=r2r1=√2−1 bulunur. Soruda r3+r4=√2 verildiğinden ve r4=r3⋅(√2−1) olduğundan r3=1r4=√2−1 bulunur. Bu değerleri (...2) ve (...3) te yerine yazarsak r1=√2+1√2−1r2=√2+1 bulunur.
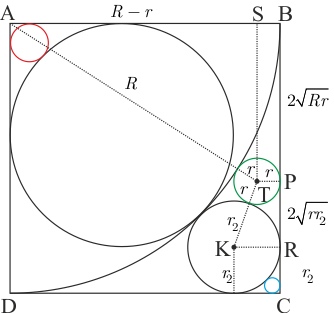
Şekildeki gibi çeyrek çemberin yarıçapına R ve yeşil çemberin yarıçapına r diyelim. |AT|=R+r ve |AS|=R−r olacağından |ST|=|BP|=2√Rr bulunur. Benzer mantık KTPR dik yamuğunda yapılırsa |PR|=2√rr2 bulunur. |RC|=r2 olduğundan, karenin bir kenarı |BC|=r2+2√r(√r2+√R) bulunur. Ayrıca karenin bir kenarı R olduğundan R=r2+2√r(√r2+√R) olur. Bu denklemden 2√r=R−r2√R+√r2⇒2√r=√R−√r2(...4) elde edilir. Bu eşitliğin karesini alırsak 4r=R+r2−2√Rr2(...5) olur. İlk şekilden görüleceği üzere |AH|=R=r1(√2+1) ve (...1) nolu eşitlikten r2=r1⋅(√2−1) değerleri (...5) te yerine yazılırsa 4r=r1(√2+1)+r1(√2−1)−2√r1(√2+1)⋅r1(√2−1) ⇒r=r1⋅√2−12(...6) bulunur. Bulduğumuz r1=√2+1√2−1 değerini yerine yazarsak r=√2+12 bulunur.
Sonuç olarak çemberlerden herhangi birinin yarıçapı ile diğer çemberlerin yarıçaplarını ifade edebilecek genellikte bir çözüm sunmuş olduk.
Soru
x∈R için x√x−2√x=1 olduğuna göre, x2−3x ifadesinin değeri kaçtır?
Çözüm
x√x−2√x−1=0 biçimine getirelim ve 2√x yerine √x+√x yazalım. x√x−√x−√x−1=0 √x(x−1)−√x−1=0√x(√x−1)(√x+1)−(√x+1)=0(√x+1)[√x.(√x−1)−1]=0(√x+1)[x−√x−1]=0 olur. Bu durumda √x=−1 veya x−√x−1=0 dır. Fakat √x=−1 olamayacağından x−√x−1=0 olur. √x i eşitliğin diğer tarafına alırsak x−1=√x olur. Bu eşitliğin her iki tarafının da karesini alırsak x2−2x+1=x⇒x2−3x=−1 bulunur.

