Hanoi kuleleri bir bulmaca olarak Fransız matematikçi Édouard Lucas tarafından 1883 yılında ortaya atılmıştır. Farklı zaman dilimlerinde çeşitli efsanalerle sunulan bir tarihi de mevcuttur. Detaylı bilgi için ilgili linklere bakınız. (Kaynaklar ingilizcedir.)
Oyun, I. kuledeki disklerin III. kuleye taşınmasından ibarettir. Fakat bunu aşağıdaki kurallara uygun yapmak zorundasınız:
- Her hamlenizde sadece bir diski hareket ettirebilirsiniz.
- Bir diskin üstüne ondan daha büyük bir disk koyamazsınız.
Başarılar:)
Soru
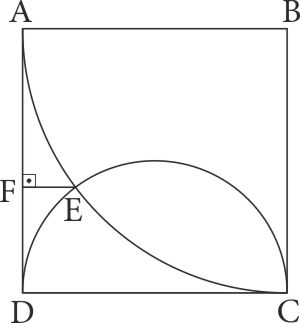
Şekilde \(B\) merkezli çeyrek çember \(ABCD\) karesine içten \(A\) ve \(C\) noktalarında; \([DC]\) çaplı yarım çember ise \(D\) ve \(C\) noktalarında teğettir. \(E\) noktası kesim noktasıdır. \([EF] \bot [AD]\) ve \(|EF|=2\) birim olduğuna göre, \(ABCD\) karesinin alanı kaç birim karedir?
Çözüm 1
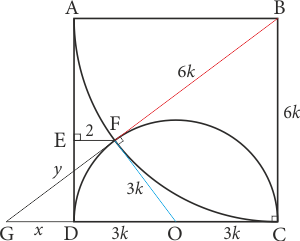
Şekildeki gibi \(BF \cap CD = \{ G\} \) olacak biçimde \([BG]\) ve \([CG]\) çizilsin. \(O\) merkezli yarım çember için \([OF]\) çizilsin. \(|OF|=|OC|=|OD|=3k\) olsun. \(B\) merkezli çeyrek çember için \(|BC|=|BF|=6k\) olur. \([BC]\), \(B\) noktasından \(O\) merkezli yarım çembere çizilen teğet ve \(|BF|=|BC|\) olduğundan \([BF]\) de \(O\) merkezli yarım çembere \(E\) de teğettir. Ek olarak \(OCBF\) dörtgeninin bir deltoid olduğu da görülebilirdi. \([OF]\perp[BG]\) gereği \(BGC \sim OGF\) olur. \(|GD|=x\) ve \(|GF|=y\) dersek benzerlik gereği \[\frac{3k}{{6k}} = \frac{y}{{x + 6k}} = \frac{{x + 3k}}{{y + 6k}}\] olur. Bu eşitlikten \(x = 2k\) ve \(y=4k\) bulunur. Demek ki \(FGO\) ve \(BCG\) üçgenleri birer 3-4-5 üçgenleriymiş.
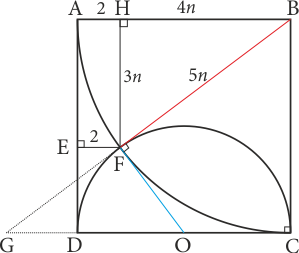
Şekildeki gibi \([FH]\perp[AB]\) çizilirse \(OFG\sim FHB\) olacağından \(FHB\) üçgeni de bir 3-4-5 üçgenidir. \(|HF|=3n\), \(|HB|=4n\) ve \(|BF|=5n\) dersek ve \(|BF|=|BA|\) eşitliği görülürse \[4n+2=5n\] olacağından \(n=2\) ve karenin bir kenar uzunluğu \(10\) birim bulunur. Böylece \[Alan(ABCD)=100\,br^2\] olur.
Çözüm 2 (Erhan Erdoğan)

Aşağıdaki videoda, kenar uzunlukları sırasıyla 3,4 ve 5 ile orantılı bir üçgenin pergel ve ölçüsüz bir cetvelle nasıl çizilebileceğine dair bir örnek yol gösteriyorum. Tabii çizim sonunda neden diye sormak gerekebilir:)

