Soru
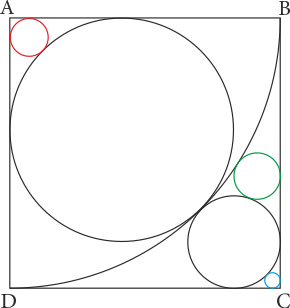 Şekildeki \(ABCD\) karesinde \(A\) merkezli çeyrek çember ile 5 çember verilmiştir. Çemberler şekildeki gibi kareye ve birbirine teğettir. Mavi ve kırmızı çemberlerlerin yarıçapları toplamı \(\sqrt 2 \) olduğuna göre, yeşil çemberin yarıçapı kaç birimdir?
Şekildeki \(ABCD\) karesinde \(A\) merkezli çeyrek çember ile 5 çember verilmiştir. Çemberler şekildeki gibi kareye ve birbirine teğettir. Mavi ve kırmızı çemberlerlerin yarıçapları toplamı \(\sqrt 2 \) olduğuna göre, yeşil çemberin yarıçapı kaç birimdir?
Çözüm
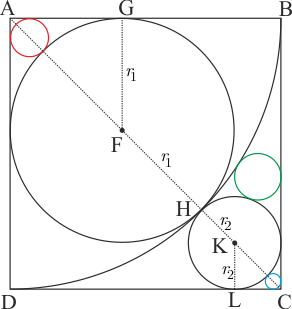
\(AGF\) üçgeninde \(|AF| = {r_1}\sqrt 2\) dir. \(KLC\) üçgeninde \(|KC|={r_2}\sqrt 2\) dir. Bu durumda \(|AC| = \left( {{r_1} + {r_2}} \right)\left( {\sqrt 2 + 1} \right)\) olur. \(|AH| = {r_1}\left( {\sqrt 2 + 1} \right)\) karenin bir kenarına eşit olduğundan \(|AC| = \sqrt 2 |AH|\) olur. O halde \(\left( {{r_1} + {r_2}} \right)\left( {\sqrt 2 + 1} \right) = \sqrt 2 {r_1}\left( {\sqrt 2 + 1} \right)\) eşitliğinden $$\dfrac{r_2}{r_1} = \sqrt{2} -1 \qquad (...1)$$ bulunur.
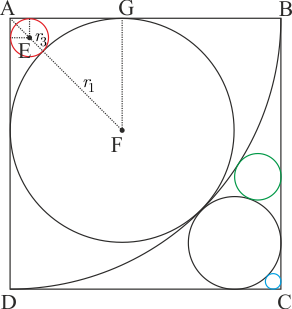
Şekildeki gibi kırmızı çemberin yarıçapına \(r_3\) dersek ve merkeziyle karenin kenarlarına dik çizip gerekli işlemleri yaparsak \(AF| = |AE| + |EF| = {r_3}\sqrt 2 + {r_3} + {r_1}\) olurken \(AGF\) üçgeninde \(|AF| = {r_1}\sqrt 2 \) olduğundan \({r_3}\sqrt 2 + {r_3} + {r_1} = {r_1}\sqrt 2 \) olur. Bu eşitlikten \[r_3=r_1.\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\qquad(...2)\] elde edilir. Benzer biçimde mavi çemberin yarıçapına \(r_4\) dersek, ilk şekilde \(|KC| = {r_2} + {r_4} + {r_4}\sqrt 2 \) bulunur. Ayrıca \(|KC| = {r_2}\sqrt 2 \) olduğundan \[r_4=r_2.\dfrac{\sqrt{2}-1}{\sqrt{2}+1}\qquad(...3)\] elde edilir. Elde ettiğimiz son iki eşitliği taraf tarafa oranlarsak \(\dfrac{{{r_4}}}{{{r_3}}} = \dfrac{{{r_2}}}{{{r_1}}} = \sqrt {2} - 1\) bulunur. Soruda \({r_3} + {r_4} = \sqrt 2 \) verildiğinden ve \({r_4} = {r_3} \cdot \left( {\sqrt {2} - 1} \right)\) olduğundan \[r_3=1 \qquad r_4=\sqrt{2}-1\] bulunur. Bu değerleri (...2) ve (...3) te yerine yazarsak \[r_1=\dfrac{\sqrt{2}+1}{\sqrt{2}-1}\qquad r_2=\sqrt{2}+1\] bulunur.
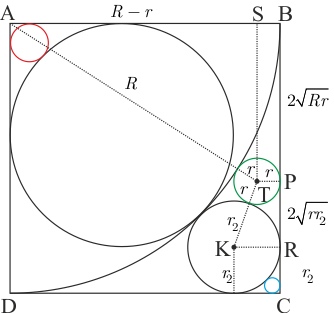
Şekildeki gibi çeyrek çemberin yarıçapına \(R\) ve yeşil çemberin yarıçapına \(r\) diyelim. \(|AT|=R+r\) ve \(|AS|=R-r\) olacağından \(|ST|=|BP|=2\sqrt{Rr}\) bulunur. Benzer mantık \(KTPR\) dik yamuğunda yapılırsa \(|PR|=2\sqrt{rr_2}\) bulunur. \(|RC|=r_2\) olduğundan, karenin bir kenarı \(|BC| = {r_2} + 2\sqrt r \left( {\sqrt {{r_2}} + \sqrt R } \right)\) bulunur. Ayrıca karenin bir kenarı \(R\) olduğundan \(R = {r_2} + 2\sqrt r \left( {\sqrt {{r_2}} + \sqrt R } \right)\) olur. Bu denklemden \[2\sqrt r = \frac{{R - {r_2}}}{{\sqrt R + \sqrt {{r_2}} }} \Rightarrow 2\sqrt r = \sqrt R - \sqrt {{r_2}} \qquad (...4)\] elde edilir. Bu eşitliğin karesini alırsak \[4r = R + {r_2} - 2\sqrt {R{r_2}}\qquad(...5)\] olur. İlk şekilden görüleceği üzere \(|AH| = R = {r_1}\left( {\sqrt 2 + 1} \right)\) ve (...1) nolu eşitlikten \({r_2} = {r_1} \cdot \left( {\sqrt 2 - 1} \right)\) değerleri (...5) te yerine yazılırsa \[4r = {r_1}\left( {\sqrt 2 + 1} \right) + {r_1}\left( {\sqrt 2 - 1} \right) - 2\sqrt {{r_1}\left( {\sqrt 2 + 1} \right) \cdot {r_1}\left( {\sqrt 2 - 1} \right)} \] \[ \Rightarrow r = {r_1} \cdot \frac{{\sqrt 2 - 1}}{2}\qquad(...6)\] bulunur. Bulduğumuz \({r_1} = \dfrac{{\sqrt 2 + 1}}{{\sqrt 2 - 1}}\) değerini yerine yazarsak \[r = \dfrac{{\sqrt 2 + 1}}{2}\] bulunur.
Sonuç olarak çemberlerden herhangi birinin yarıçapı ile diğer çemberlerin yarıçaplarını ifade edebilecek genellikte bir çözüm sunmuş olduk.
Soru
\(x \in R\) için \(x\sqrt x - 2\sqrt x = 1\) olduğuna göre, \[{x^2} - 3x\] ifadesinin değeri kaçtır?
Çözüm
\(x\sqrt x - 2\sqrt x - 1 = 0\) biçimine getirelim ve \(2\sqrt x\) yerine \(\sqrt x + \sqrt x \) yazalım. \[x\sqrt x - \sqrt x - \sqrt x - 1 = 0\] \[\sqrt x (x - 1) - \sqrt x - 1 = 0\]\[\sqrt x (\sqrt x - 1)(\sqrt x + 1) - (\sqrt x + 1) = 0\]\[(\sqrt x + 1)\left[ {\sqrt x .(\sqrt x - 1) - 1} \right] = 0\]\[(\sqrt x + 1)\left[ {x - \sqrt x - 1} \right] = 0\] olur. Bu durumda \(\sqrt x = - 1\) veya \(x - \sqrt x - 1 = 0\) dır. Fakat \(\sqrt x = - 1\) olamayacağından \(x - \sqrt x - 1 = 0\) olur. \(\sqrt{x}\) i eşitliğin diğer tarafına alırsak \[x - 1 = \sqrt x \] olur. Bu eşitliğin her iki tarafının da karesini alırsak \[\begin{array}{l}{x^2} - 2x + 1 = x\\ \Rightarrow {x^2} - 3x = - 1\end{array}\] bulunur.

