Örnek 1

200 kişinin okuduğu Hacettepe Hukuk öğrencilerinin kümesini $H$ sembolize etsin. Böylece öğrencilerin oluşturduğu bu kümenin eleman sayısı $|H| = 200$ olur. Bu öğrencilerden $95$ tanesi İnsan Hakları Hukuku dersini, $48$ tanesi de Spor Hukuku dersini alıyor olsun. İnsan hakları hukuku dersini alanların oluşturduğu kümeyi $k_1$ ile Spor hukuku dersini alanların oluşturduğu kümeyi de $k_2$ ile gösterelim. Böylece $s\left( {{k_1}} \right) = 95$ ve $s\left( {{k_2}} \right) = 48$ olur. Ayrıca her iki dersi de alan $20$ öğrenci olsun. Bunların oluşturduğu kümeyi de ${k_1}{k_2}$ ile gösterelim. Yani $s\left( {{k_1}{k_2}} \right) = 20$ dir. Bu durumda İnsan hakları hukuku veya spor hukuku dersini alan öğrencilerin oluşturduğu kümenin eleman sayısı $$s\left( {{k_1}{\rm{ veya }}{k_2}} \right) = s\left( {{k_1}} \right) + s\left( {{k_2}} \right) - s\left( {{k_1}{k_2}} \right) = 95 + 48 - 20 = 123$$ olur. Ayrıca insan hakları dersini almayanların oluşturduğu kümeyi $\overline {{k_1}}$ ile gösterirsek, $s\left( {\overline {{k_1}} } \right) = 200 - 95 = 105$ ; spor hukuku dersini almayanların oluşturduğu kümeyi de $\overline {{k_2}}$ ile gösterirsek $s\left( {\overline {{k_2}} } \right) = 200 - 48 = 152$ olacaktır. Son olarak her iki dersi de almayanların oluşturduğu kümeyi $\overline {{k_1}} \overline {{k_2}}$ ile gösterirsek, bu kümenin eleman sayısı da $$\begin{array}{l} \\  & s\left( {\overline {{k_1}} \overline {{k_2}} } \right) = |H| - s\left( {{k_1}{\rm{ veya }}{k_2}} \right)\\  &  = |H| - \left[ {s\left( {{k_1}} \right) + s\left( {{k_2}} \right)} \right] + s\left( {{k_1}{k_2}} \right)\\  &  = 200 - 123\\  &  = 77 \end{array}$$ olur.

Yazdığımız $s\left( {\overline {{k_1}} \overline {{k_2}} } \right) = |H| - \left[ {s\left( {{k_1}} \right) + s\left( {{k_2}} \right)} \right] + s\left( {{k_1}{k_2}} \right)$ eşitliğini biraz daha soyut biçimde yorumlamaya çalışalım. Bu $200$ kişi arasından herhangi biri bu derslerin ikisini de almıyorsa hem $s\left( {\overline {{k_1}} \overline {{k_2}} } \right)$ içinde hem de $|H|$  içinde sayılır. Böylece bu kişiler için eşitlik sağlanır, çünkü bu sayımda $1=1$ olacaktır. Öte yandan eğer bu $200$ kişi arasından herhangi biri bu derslerden sadece birini alıyorsa – örneğin insan hakları hukuku dersini – bu durumda eşitliğin solunda sayılmaz, fakat $1$ kez $|H|$ içinde, $1$ kez de $s\left( {{k_1}} \right)$ yer sayılır. Dolayısıyla eşitlik yine sağlanır çünkü $0=1-1$ olur. Son olarak, $200$ kişi arasından herhangi biri bu derslerin her ikisini de alıyorsa eşitliğin solunda yine sayılmaz, fakat sağındaki her küme içinde $1$ kez sayılır. Bu durumda da eşitlik tekrar sağlanır. Çünkü $0 = 1 - \left( {1 + 1} \right) + 1 = \left( {\begin{array}{*{20}{c}} 2\\ 0 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 2\\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 2\\ 2 \end{array}} \right)$ dir. Böylece eşitliğin genel olarak $k_1$ ve $k_2$ gibi koşullu durumlar için daima sağlanacağını göstermiş olduk.

Örnek 2

Birinci örnekteki iki derse ek olarak 36 kişinin de Fransızca dersini, 10 kişinin hem Fransızca hem de İnsan hakları hukuku dersini, 7 kişinin hem Fransızca hem de Spor hukuku dersini ve 15 kişinin de bu üç dersi aldığını düşünelim. Fransızca dersini alan öğrencilerin oluşturduğu kümeyi de $k_3$ ile gösterirsek $s\left( {{k_3}} \right) = 36$, $s\left( {{k_1}{k_3}} \right) = 10$, $s\left( {{k_2}{k_3}} \right) = 7$ ve $s\left( {{k_1}{k_2}{k_3}} \right) = 15$ yazılabilir. Bu durumda bu üç dersin hiçbirini almayanların oluşturduğu kümenin elaman sayısı $$\begin{align*} s\left( {\overline {{k_1}} \overline {{k_2}} \overline {{k_3}} } \right) &= |H| - \left[ {s\left( {{k_1}} \right) + s\left( {{k_2}} \right) + s\left( {{k_3}} \right)} \right]\\& + \left[ {s\left( {{k_1}{k_2}} \right) + s\left( {{k_1}{k_3}} \right) + s\left( {{k_2}{k_3}} \right)} \right] - s\left( {{k_1}{k_2}{k_3}} \right)\\ &  = 200 - \left[ {95 + 48 + 36} \right] + \left[ {20 + 10 + 7} \right] - 15\\ &  = 43 \end{align*}$$ bulunur. Yazdığımız bu son eşitlik bir Venn şeması çizilerek elde edilebilir. Ayrıca lise seviyesinde kümeler konusunda gösterilen bir eşitlik olduğu da hatırlanabilir. Birinci örnekte olduğu gibi bu eşitliği de biraz soyut biçimde yorumlayalım.

• 200 kişi arasından herhangi biri bu derslerden hiçbirini almıyorsa eşitliğinde solunda $s\left( {\overline {{k_1}} \overline {{k_2}} \overline {{k_3}} } \right)$ ve sağında $|H|$ içinde 1 er kez sayılacağı için eşitlik sağlanacaktır.
• 200 kişi arasından herhangi biri bu derslerden sadece birini alıyorsa – örneğin Fransızca – eşitliğin solunda sayılmayacak ama sağında 1 kez $|H|$ içinde 1 kez de $s\left( {{k_3}} \right)$ içinde sayılacağından eşitlik tekrar sağlanacaktır. ($0 = 1 - 1$)
• 200 kişi arasından herhangi biri bu derslerden herhangi ikisini alıyorsa – örneğin Fransızca ve Spor hukuku– eşitliğin solunda sayılmayacak ama sağında 1 er kez $|H|$, $s\left( {{k_3}} \right)$, $s\left( {{k_2}} \right)$ ve $s\left( {{k_2}{k_3}} \right)$ içinde sayılacağından eşitlik tekrar sağlanacaktır. ($0 = 1 - \left( {1 + 1} \right) + 1$)
• Son olarak 200 kişi arasından herhangi biri bu derslerden her üçünü de alıyorsa eşitliğin solunda sayılmayacak ama sağındaki her küme içinde 1 er sayılacağından eşitlik tekrar sağlanacaktır, çünkü bu durumda da $0 = 1 - \left[ {1 + 1 + 1} \right] + \left[ {1 + 1 + 1} \right] - 1 = \left( {\begin{array}{*{20}{c}} 3\\ 0 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 3\\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 3\\ 2 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 3\\ 3 \end{array}} \right)$

Böylece sonlu bir $H$ kümesinin $k_1$, $k_2$ ve $k_3$ koşullu üç alt kümesinin hiçbirinde bulunmayan elemanların oluşturduğu kümenin eleman sayısı için yukarıdaki eşitliğin daima doğru olduğu göstermiş olduk.

Örnek 3

İlk iki örnekten faydalanırsak, sonlu bir $H$ kümesinin $k_1$, $k_2$, $k_3$ ve $k_4$ gibi dört altkümesinin hiçbirinde bulunmayan elemanların oluşturduğu kümenin eleman sayısının $$\begin{align*} s\left( {\overline {{k_1}} \overline {{k_2}} \overline {{k_3}} \overline {{k_4}} } \right) &= |H| - \left[ {s\left( {{k_1}} \right) + s\left( {{k_2}} \right) + s\left( {{k_3}} \right) + s\left( {{k_4}} \right)} \right]\\ & + \left[ {s\left( {{k_1}{k_2}} \right) + s\left( {{k_1}{k_3}} \right) + s\left( {{k_1}{k_4}} \right) + s\left( {{k_2}{k_3}} \right) + s\left( {{k_2}{k_4}} \right) + s\left( {{k_3}{k_4}} \right)} \right]\\ & - \left[ {s\left( {{k_1}{k_2}{k_3}} \right) + s\left( {{k_1}{k_2}{k_4}} \right) + s\left( {{k_1}{k_3}{k_4}} \right) + s\left( {{k_2}{k_3}{k_4}} \right)} \right]\\ & + s\left( {{k_1}{k_2}{k_3}{k_4}} \right) \end{align*}$$ eşitliği ile gösterebiliriz. Bunu kanıtlamak için $H$ kümesinin rastgele bir $x$ elemanını düşünelim.

• Eğer $x$ bu alt kümelerden birinde değilse, 1 kez eşitliğin solunda 1 kez de $H$ kümesinde sayılır.
• Eğer $x$ bu alt kümelerden sadece birinde – örneğin $k_1$ – ise, eşitliğin solunda sayılmaz, fakat 1 kez $H$ kümesinde, 1 kez de $k_1$ de sayılır. Yani toplamda $1-1=0$ olup, eşitlik doğrulanır.
• Eğer $x$ bu alt kümelerden sadece ikisinde – örneğin sadece $k_1$ ve $k_2$ de – ise, eşitliğin solunda sayılmaz, fakat 1 er kez $H$, $k_1$, $k_2$ ve $k_{1}k_{2}$ kümelerinde sayılır. Yani toplamda $1 - \left[ {1 + 1} \right] + 1 = \left( {\begin{array}{*{20}{c}} 2\\ 0 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 2\\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 2\\ 2 \end{array}} \right) = 0$ olup, eşitlik doğrulanır.
• Eğer $x$ bu alt kümelerden sadece üçünde – örneğin sadece $k_1$, $k_2$ ve $k_3$ te  – ise, eşitliğin solunda sayılmaz, fakat 1 er kez $H$, $k_1$, $k_2$, $k_3$, $k_{1}k_{2}$, $k_{1}k_{3}$, $k_{2}k_{3}$ ve $k_{1}k_{2}k_{3}$ kümelerinde sayılır. Yani toplamda $1 - \left[ {1 + 1 + 1} \right] + \left[ {1 + 1 + 1} \right] - 1 = \left( {\begin{array}{*{20}{c}} 3\\ 0 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 3\\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 3\\ 2 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 3\\ 3 \end{array}} \right) = 0$ olup, eşitlik doğrulanır.
• Eğer $x$ bu alt kümelerden hepsinde ise, eşitliğin solunda sayılmaz, fakat eşitliğin sağındaki 16 kümenin her birinde 1 er kez sayılır. Yani toplamda $$\begin{array}{l} 1 - \left[ {1 + 1 + 1 + 1} \right] + \left[ {1 + 1 + 1 + 1 + 1 + 1} \right] - \left[ {1 + 1 + 1 + 1} \right] + 1\\  = \left( {\begin{array}{*{20}{c}} 4\\ 0 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 4\\ 1 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 4\\ 2 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} 4\\ 3 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 4\\ 4 \end{array}} \right)\\  = 0 \end{array}$$ olup, eşitlik doğrulanır.

Böylece eşitliğin her iki tarafının da herhangi bir $x$ elemanını eşit biçiminde saydığını göstererek eşitliğin doğru olduğunu kanıtlamış olduk.

Teorem

Eleman sayısı $S$ olan bir $H$ kümesinin $1 \le i \le n$ için birbirinden farklı $k_i$ alt kümelerinden hiçbirinde yer almayan elemanlarının sayısını $\overline S  = s\left( {\overline {{k_1}} \overline {{k_2}} \overline {{k_3}} ...\overline {{k_n}} } \right)$ ile gösterirsek $$\begin{align*} \overline S  &  = S - \left[ {s\left( {{k_1}} \right) + s\left( {{k_2}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_n}} \right)} \right]\\  &  + \left[ {s\left( {{k_1}{k_2}} \right) + s\left( {{k_1}{k_3}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_1}{k_n}} \right) + s\left( {{k_2}{k_3}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_{n - 1}}{k_n}} \right)} \right]\\  &  - [s\left( {{k_1}{k_2}{k_3}} \right) + s\left( {{k_1}{k_2}{k_4}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_1}{k_2}{k_n}} \right) + s\left( {{k_1}{k_3}{k_4}} \right)\\  &  +  \cdot  \cdot  \cdot  + s\left( {{k_1}{k_3}{k_n}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_{n - 2}}{k_{n - 1}}{k_n}} \right)]\\  &  +  \cdot  \cdot  \cdot  + {\left( { - 1} \right)^n}s\left( {{k_1}{k_2}...{k_n}} \right) \end{align*}$$ veya  $$\begin{align*} \overline S  & = S - \sum\limits_{1 \le i \le n} {\left[ {s\left( {{k_i}} \right)} \right]} \\  &  + \sum\limits_{1 \le i < j \le n} {\left[ {s\left( {{k_i}{k_j}} \right)} \right]} \\  &  - \sum\limits_{1 \le i < j < t \le n} {\left[ {s\left( {{k_i}{k_j}{k_t}} \right)} \right]} \\  &  +  \cdot  \cdot  \cdot \\  &  + {\left( { - 1} \right)^n}s\left( {{k_1}{k_2}...{k_n}} \right) \end{align*}$$ olur.

Kanıt:

Tümevarım yöntemiyle bir kanıt verilebilir. Fakat yukarıdaki örneklerde kullandığımız kanıtların benzerini yapacağız. $H$ kümesinin bir $x$ elemanı bu alt kümelerden hiçbirinde değilse, eşitliğin solunda $\overline S$ ve sağında $S$ içinde 1 er kez sayılırken diğer kümelerde sayılmazlar. Böylece eşitlik bu durumda sağlanır. Diyelim ki $x$ elemanı verilen alt kümelerden $r$ tanesinin elemanı olsun. Bu durumda eşitliğinde solunda bu eleman sayılmaz. Fakat

1. Bir kez $S$ de sayılır.
2. $r$ kez $\sum\limits_{1 \le i \le n} {\left[ {s\left( {{k_i}} \right)} \right]}$ de sayılır.
3. $\left( {\begin{array}{*{20}{c}} r\\ 2 \end{array}} \right)$ kez $\sum\limits_{1 \le i < j \le n} {\left[ {s\left( {{k_i}{k_j}} \right)} \right]}$ de sayılır. ($r$ alt kümeden seçilen 2 alt kümenin kesişimleri)
4. $\left( {\begin{array}{*{20}{c}} r\\ 3 \end{array}} \right)$ kez $\sum\limits_{1 \le i < j < t \le n} {\left[ {s\left( {{k_i}{k_j}{k_t}} \right)} \right]}$ de sayılır. ($r$ alt kümeden seçilen 3 alt kümenin kesişimleri)
    ................................................
5. $\left( {\begin{array}{*{20}{c}} r\\ r \end{array}} \right)=1$ kez $\sum {s\left( {{k_{{i_1}}}{k_{{i_2}}}{k_{{i_3}}}...{k_{{i_r}}}} \right)}$ de sayılır.

Sonuç olarak $x$ elemanı eşitliğin sağında (binom açılımı gereği) $$1 - r + \left( {\begin{array}{*{20}{c}} r\\ 2 \end{array}} \right) - \left( {\begin{array}{*{20}{c}} r\\ 3 \end{array}} \right) +  \cdot  \cdot  \cdot  + {\left( { - 1} \right)^r}\left( {\begin{array}{*{20}{c}} r\\ r \end{array}} \right) = {\left[ {1 + \left( { - 1} \right)} \right]^r} = 0$$ kez sayılır.

Böylece eşitliğin herhangi bir $x$ elemanını her iki tarafında da eşit saydığını göstermiş oluruz.

Farklı örneklere geçmeden önce gösterim biçimi olarak $${S_0} = S$$ $${S_1} = \left[ {s\left( {{k_1}} \right) + s\left( {{k_2}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_n}} \right)} \right]$$ $${S_2} = \left[ {s\left( {{k_1}{k_2}} \right) + s\left( {{k_1}{k_3}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_1}{k_n}} \right) + s\left( {{k_2}{k_3}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_{n - 1}}{k_n}} \right)} \right]$$ ve genel olarak  $${S_k} = \sum {s\left( k_{i_1}k_{i_2}k_{i_3}...k_{i_r} \right)} , \qquad (1 \le r \le n)$$ seçersek $$\overline S  = {S_0} - {S_1} + {S_2} - {S_3} +  \cdot  \cdot  \cdot  + {\left( { - 1} \right)^n}{S_n}$$ biçimini alır.

Örnek 5

$x_1$, $x_2$, $x_3$ ve $x_4$ doğal sayıları için ${x_1} + {x_2} + {x_3} + {x_4} = 15$ ve ${x_i} \le 6$ ($i \in \left\{ {1,2,3,4} \right\}$) koşullarını sağlayan kaç farklı $\left( {{x_1},{x_2},{x_3},{x_4}} \right)$ sıralı dörtlüsü vardır?

Çözüm

Tekrarlı gruplandırma (kombinasyon) gereği sadece ${x_1} + {x_2} + {x_3} + {x_4} = 15$ eşitliğini sağlayan $\left( {\begin{array}{*{20}{c}} {15 + 4 - 1}\\ {4 - 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {18}\\ 3 \end{array}} \right)$ kadar sıralı dörtlü yazılabilir. Diğer koşulu sağlamak için ${k_i}$ alt kümesi ${x_i} \ge 7$ olacak biçimde tanımlayalım. Simetri gereği $s\left( {{k_1}} \right) = s\left( {{k_2}} \right) = s\left( {{k_3}} \right) = s\left( {{k_4}} \right)$ olacaktır. ${k_i}$ alt kümesinin eleman sayısını bulmak için ${x_i}$ değerini 7 den başlatmamız gerekir. Böylece ${x_1} + {x_2} + {x_3} + {x_4} = 8$ denkleminin çözüm sayısı $s\left( {{k_1}} \right) = \left( {\begin{array}{*{20}{c}} {8 + 4 - 1}\\ {4 - 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {11}\\ 3 \end{array}} \right)$ olur. Böylece, ${S_1} = 4 \cdot \left( {\begin{array}{*{20}{c}} {11}\\ 3 \end{array}} \right)$ olur. Benzer biçimde $x_1$ ve $x_2$ değerlerinin her ikisini de 7 den başlatırsak, $s\left( {{k_1}{k_2}} \right)$ değeri ${x_1} + {x_2} + {x_3} + {x_4} = 4$ denkleminin çözüm sayısı olur. Böylece, $s\left( {{k_1}{k_2}} \right) = \left( {\begin{array}{*{20}{c}} {1 + 4 - 1}\\ {4 - 1} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 4\\ 3 \end{array}} \right)$ olurken, ${S_2} = \left( {\begin{array}{*{20}{c}} 4\\ 2 \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} 4\\ 3 \end{array}} \right)$ olur. Ayrıca, $x_i$ değerlerinden üçünü birden 7 den başlatamayacağımızdan $s\left( {{k_i}{k_j}{k_t}} \right) = 0$ ve $s\left( {{k_1}{k_2}{k_3}{k_4}} \right) = 0$ dır. O halde istenilen koşulları sağlayan dörtlülerin sayısı $$\begin{align*} s\left( {\overline {{k_1}} \overline {{k_2}} \overline {{k_3}} \overline {{k_4}} } \right)  & = {S_0} - {S_1} + {S_2} - {S_3} + {S_4} \\  & = \left( {\begin{array}{*{20}{c}}  {18}\\  3  \end{array}} \right) - 4 \cdot \left( {\begin{array}{*{20}{c}}  {11}\\  3  \end{array}} \right) + \left( {\begin{array}{*{20}{c}}  4\\  2  \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}}  4\\  3  \end{array}} \right) - 0 + 0 \\  & =180 \end{align*}$$ bulunur.

Örnek 6 (Örten Fonksiyon Sayısı)

$m \ge n$ olmak üzere, $A = \left\{ {{a_1},{a_2}, \cdot  \cdot  \cdot ,{a_m}} \right\}$ ve $B = \left\{ {{b_1},{b_2}, \cdot  \cdot  \cdot ,{b_n}} \right\}$ sonlu kümelerinde $A$ dan $B$ ye kaç farklı örten fonksiyon tanımlanabilir?

Çözüm:

$f:A \to B$ olacak biçimde $A$ dan $B$ ye ${n^m}$ farklı $f$ fonksiyonunun tanımlanabileceğini biliyoruz. Bu durumda $S = {S_0} = {n^m}$ olsun. $1 \le i \le n$ olmak üzere $A$ dan $B$ ye tanımlı tüm fonksiyonlar kümesinin $b_i$ elemanını içermeyen alt kümesini $k_i$ olarak tanımlayalım. Bu durumda $k_i$ kümesindeki fonksiyonların değer kümesinde $b_i$ elemanı yer almaz. Böylece $s\left( {\overline {{k_i}} } \right)$, değer kümesinde $b_i$ elemanı bulunan fonksiyonların sayısını vereceğinden, $A$ dan $B$ ye tanımlı örten fonksiyon sayısı $s\left( {\overline {{k_1}} \overline {{k_2}}  \cdot  \cdot  \cdot \overline {{k_n}} } \right)$ olur. Dikkat edilirse $B$ kümesinden $b_i$ elemanını çıkardığımız için $s\left( {{k_i}} \right) = {\left( {n - 1} \right)^m}$ dir. Benzer biçimde $1 \le i < j \le n$ olmak üzere, $b_i$ ve $b_j$ elemanlarını değer kümesinde içermeyen fonksiyon sayısı $s\left( {{k_i}{k_j}} \right) = {\left( {n - 2} \right)^m}$ dir. Böylece $${S_1} = \left[ {s\left( {{k_1}} \right) + s\left( {{k_2}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_n}} \right)} \right] = n \cdot {\left( {n - 1} \right)^m}$$ ve $${S_2} = \left[ {s\left( {{k_1}{k_2}} \right) +  \cdot  \cdot  \cdot  + s\left( {{k_{n - 1}}{k_n}} \right)} \right] = \left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right) \cdot {\left( {n - 2} \right)^m}$$ dir. Genel olarak, $1 \le r \le n$ olmak üzere, $${S_r} = \sum\limits_{1 \le {i_1} < {i_2} <  \cdot  \cdot  \cdot  < {i_r} \le n} {s\left( {{k_{{i_1}}}{k_{{i_2}}} \cdot  \cdot  \cdot {k_{{i_r}}}} \right)}  = \left( {\begin{array}{*{20}{c}} n\\ r \end{array}} \right) \cdot {\left( {n - r} \right)^m}$$ dir. Bu durumda $A$ dan $B$ ye örten fonksiyon sayısı $$\begin{align*} s\left( {\overline {{k_1}} \overline {{k_2}}  \cdot  \cdot  \cdot \overline {{k_n}} } \right)  &  = {S_0} - {S_1} + {S_2} - {S_3} +  \cdot  \cdot  \cdot  + {\left( { - 1} \right)^n}{S_n}\\  &  = {n^m} - \left( {\begin{array}{*{20}{c}} n\\ 1 \end{array}} \right) \cdot {\left( {n - 1} \right)^m} + \left( {\begin{array}{*{20}{c}} n\\ 2 \end{array}} \right) \cdot {\left( {n - 2} \right)^m} - \left( {\begin{array}{*{20}{c}} n\\ 3 \end{array}} \right) \cdot {\left( {n - 3} \right)^m}\\  &  +  \cdot  \cdot  \cdot  + {\left( { - 1} \right)^n} \cdot {\left( {n - n} \right)^m}\\  &  = \sum\limits_{i = 0}^n {{{\left( { - 1} \right)}^i}\left( {\begin{array}{*{20}{c}} n\\ i \end{array}} \right){{\left( {n - i} \right)}^m}} \end{align*}$$ olarak bulunur.

Örneğin 4 elemanlı bir $A$ kümesinden 3 elemanlı bir $B$ kümesine tanımlanabilecek örten fonksiyon sayısı $m=4$ ve $n=3$ için $$\begin{align*} s\left( {\overline {{k_1}} \overline {{k_2}} \overline {{k_3}} } \right)  & = {S_0} - {S_1} + {S_2} - {S_3}\\  & = \sum\limits_{i = 0}^3 {{{\left( { - 1} \right)}^i}\left( {\begin{array}{*{20}{c}} 3\\ i \end{array}} \right){{\left( {3 - i} \right)}^4}} \\  & = {3^4} - \left( {\begin{array}{*{20}{c}} 3\\ 1 \end{array}} \right) \cdot {2^4} + \left( {\begin{array}{*{20}{c}} 3\\ 2 \end{array}} \right) \cdot {1^4} - \left( {\begin{array}{*{20}{c}} 3\\ 3 \end{array}} \right) \cdot 0\\  & = 36 \end{align*}$$ olur.

Örnek 7 (Evli Çiftler)

4 evli çift yuvarlak bir masa etrafında herhangi karı-koca yanyana gelmeyecek biçimde kaç farkı biçimde oturabilir?

Çözüm:

Öncelikle $1 \le i \le 4$ olmak üzere, $k_i$ ile $i.$ karı-kocanın yanyana oturduğu durumları ifade edelim. Bu durumda bunları 1 kişi gibi sayıp, toplamda 7 kişiyi yuvarlak bir masa etrafında sıralamış oluruz. Tabii karı-kocanın kendi arasındaki 2 farklı biçimde yer değiştirme durumlarını da göz önüne almamız gerekir. O halde $s\left( {{k_i}} \right) = 2 \cdot \left( {7 - 1} \right)! = 2 \cdot 6!$ olur. Bu durumda ${S_1} = \left( {\begin{array}{*{20}{c}} 4\\ 1 \end{array}} \right) \cdot 2 \cdot 6!$ dir. Benzer biçimde 2 çiftin birlikte oturduğu durum sayısı ${S_2} = \left( {\begin{array}{*{20}{c}} 4\\ 2 \end{array}} \right) \cdot {2^2} \cdot 5!$ olur. 3 çiftin yanyana oturduğu durum sayısı ${S_3} = \left( {\begin{array}{*{20}{c}} 4\\ 3 \end{array}} \right) \cdot {2^3} \cdot 4!$ ve tüm çiftlerin yanyana oturduğu durum sayısı ${S_4} = \left( {\begin{array}{*{20}{c}} 4\\ 4 \end{array}} \right) \cdot {2^4} \cdot 3!$ dir. Ayrıca koşulsuz bu 8 kişinin yuvarlak masada oturma sayısı da ${S_0} = 7!$ dir. O halde, $$\begin{align*} s\left( {\overline {{k_1}} \overline {{k_2}} \overline {{k_3}} \overline {{k_4}} } \right)  & = {S_0} - {S_1} + {S_2} - {S_3} + {S_4}\\  & = 7! - \left( {\begin{array}{*{20}{c}} 4\\ 1 \end{array}} \right) \cdot 2 \cdot 6! + \left( {\begin{array}{*{20}{c}} 4\\ 2 \end{array}} \right) \cdot {2^2} \cdot 5! - \left( {\begin{array}{*{20}{c}} 4\\ 3 \end{array}} \right) \cdot {2^3} \cdot 4! + \left( {\begin{array}{*{20}{c}} 4\\ 4 \end{array}} \right) \cdot {2^4} \cdot 3!\\  & = 5040 - 5760 + 2880 - 768 + 96\\  & = 1488 \end{align*}$$ bulunur.

Örnek 1

Koordinat düzleminde $(0,0)$ noktasında başlayan iki tür hareket tanımlayalım:

$$S:(x,y) \to (x + 1,y)$$ $$Y:(x,y) \to (x,y + 1)$$

S hareketinin 1 birim sağa ve Y hareketinin de 1 birim yukarı olduğunu görüyoruz. Bu hareketleri kullanarak $(0,0)$ noktasından $(5,5)$ noktasına kaç farklı biçimde gidebileceğimizi hesaplamak istersek, 5 adet S ve 5 adet Y kullanmamız gerektiğini görürüz. Bu durumda 5 adet S ve 5 adet Y harfinin her bir farklı sıralaması bir gidiş belirtecektir. O halde toplam gidiş sayısı $\dfrac{{10!}}{{5! \cdot 5!}} = \left( {\begin{array}{*{20}{c}} {10}\\5\end{array}} \right)$ kadardır. Şimdi kendimize bir kısıt getirelim ve herhangi bir hareketin $y = x$ doğrusuna dokunabileceğini ama üstüne çıkamayacağını şart koşalım.

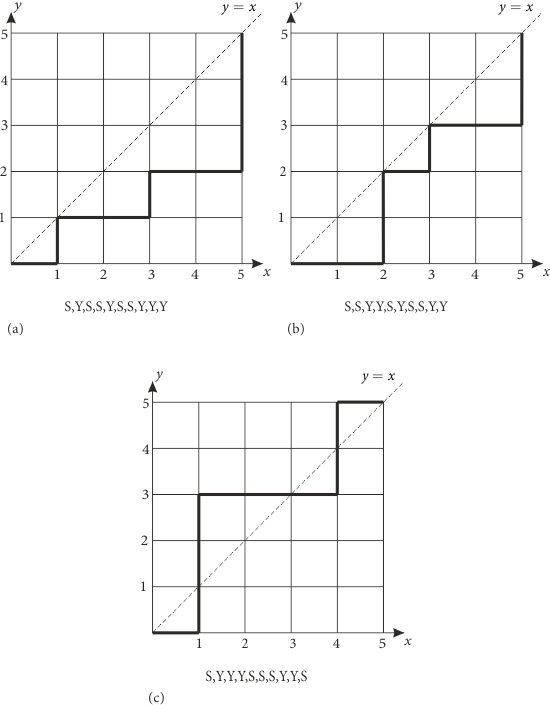
Yukarıdaki şekillerden (a) ve (b) koşulu sağlarken (c) sağlamamaktadır. Koşulumuzda ilk göze çarpan şey herhangi bir gidişin S ile başlayıp Y ile bitmesi gerektiğidir. Ayrıca herhangi bir noktaya kadar yapılan S sayısının Y sayısından az olmayacağı da (a) ve (b) şekillerden gözlemlenebilir. Yani herhangi bir gidişte $S \ge Y$ dir. (c) şeklinde böyle bir durumun olmadığı da görülebilir. Bu durumların sayısı elde edebilmek için (c) deki gibi koşula uymayan yani $y = x$ doğrusunun üstünde kalan yolların sayısını elde edip tüm durumdan çıkarabiliriz. (c) deki yolun ne zaman ilk olarak $S \ge Y$ koşulunu bozduğu yerin 3. hareketten sonra olduğuna dikkate edin. Bunu hareket diziliminde bir çizgi ile gösterirsek

$$S,Y,Y{\rm{ }}|{\rm{ }}Y,S,S,S,Y,Y,S$$

olacaktır. Şimdi bu dizilime aşağıdaki gibi bir dönüşüm uygulayalım.

$${\mathop{\rm S}\nolimits} ,Y,Y \,\,|\,\, Y,S,S,S,Y,Y,S \Leftrightarrow {\mathop{\rm S}\nolimits} ,Y,Y \,\,|\,\, S,Y,Y,Y,S,S,Y$$

Bu dönüşüm, koşulun bozulduğu ilk andan sonraki hareketleri birbiriyle değiştirmektedir. Yani Y yerine S, S yerine de Y hareketi seçilmektedir. Bu sayede hareket diziliminde 4 adet S ve 6 adet Y olmaktadır. (c) deki bu dönüşüm (d) şeklinde gösterilmektedir. Koşula aykırı bir diğer farklı yolda (e) şeklinde gösterilmektedir. Dönüşümle değişmiş biçimi de (f) de yer almaktadır. Yine 4 adet S ve 6 adet Y hareketi mevcuttur.

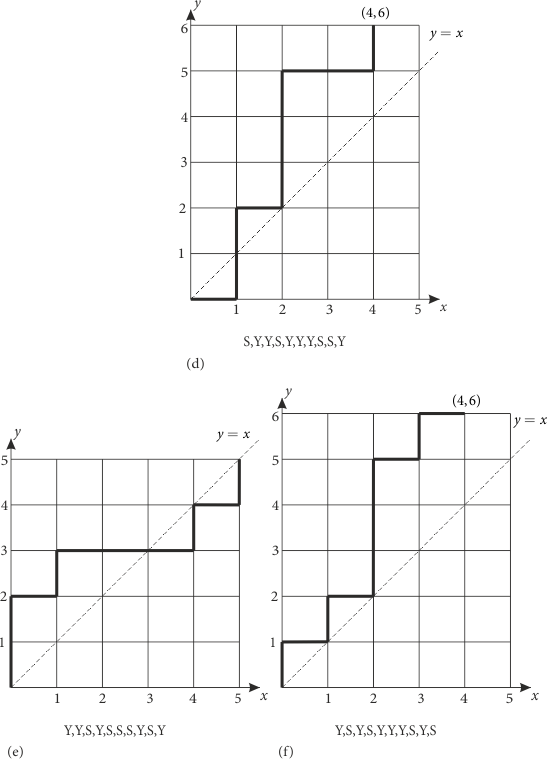
Şimdi 4 S ve 6 Y den oluşan bir hareket dizilimi olarak

$$S,Y,S,S,Y,Y,Y{\rm{ }}|{\rm{ }}Y,Y,S$$

dizilimine bakalım. Y lerin S lerden fazla olduğu ilk hareketten sonrasını çizgi ile ayırmış durumdayız. Bu dizilime dönüşüm uygularsak

$$S,Y,S,S,Y,Y,Y{\rm{ }}|{\rm{ }}S,S,Y$$

eldedilir. Dikkat ederseniz bu 5 S ve 5 Y den oluşan ama koşulumuza aykırı olan bir dizilimdir. Özetle uyguladığımız dönüşümle elde edilen her bir dizilim esasında koşula aykırı bir dizilime denktir. Yani bu biçimde $\dfrac{{10!}}{{4! \cdot 6!}} = C(10,4)$ hareket dizilimi vardır. O halde koşula uygun

$$C(10,5) - C(10,6) = 42$$

gidiş vardır.

Yukarıdaki örnekle şöyle bir genelleme elde edebiliriz:

$n \ge 0$ olmak üzere, $y=x$ doğrusu üzerine çıkmadan $(0,0)$ noktasından $(5,5)$ noktasına $n$ adet S ve $n$ adet Y hareketi ile yapılabilecek yol sayısı

$${b_n} = C(2n,n) - C(2n,n - 1) = \frac{1}{{n + 1}} \cdot C(2n,n), \quad n \ge 1, \quad b_0=1$$

olur. ${b_0},{b_1},{b_2}, \cdot  \cdot  \cdot$ sayılarına ismini Belçikalı matematikçi Eugene Charles Catalan ‘dan alan Catalan sayıları denir. Eugene, bu sayıları ${x_1}{x_2}{x_3}...{x_n}$ çarpımını  kaç farklı biçimde paranteze alabileceğini hesaplamak için kullanmıştır. Örneğin ${x_1}{x_2}{x_3}{x_4}$ çarpımını ${b_3} = 5$ farklı biçimde paranteze alabiliriz:

$$\left( {\left( {\left( {{x_1}{x_2}} \right){x_3}} \right){x_4}} \right) \quad \left( {\left( {{x_1}\left( {{x_2}{x_3}} \right)} \right){x_4}} \right) \quad \left( {\left( {{x_1}{x_2}} \right)\left( {{x_3}{x_4}} \right)} \right) \quad \left( {{x_1}\left( {\left( {{x_2}{x_3}} \right){x_4}} \right)} \right) \quad  \left( {{x_1}\left( {{x_2}\left( {{x_3}{x_4}} \right)} \right)} \right)$$

Örnek 2

Yukarıdaki örnekle özünde aynı ama cümleleri değişik olan aşağıdaki örnekleri inceleyelim.

• 3 adet 1 ve 3 adet – 1 kullanarak elde edilen dizilimlerden ${b_3} = 5$ tanesinde herhangi bir sayıdan önceki sayıların toplamın negatif değildir.

  1, 1, 1, -1, -1, -1       1, 1, -1, -1, 1, -1       1, -1, 1, 1, -1, -1

  1, 1, -1, 1, -1, -1       1, -1, 1, -1, 1, -1

   

• 4 adet 1 ve 4 adet 0 kullanılarak elde edilen dizilimlerin ${b_4} = 14$ tanesinde, soldan sağa okunurken, 0 sayısı 1 sayısını geçmez.

  10101010    10101100    10110010

  10110100    10111000    11001010

  11001100    11010010    11010100

  11011000    11100010    11100100

  11101000    11110000

   

• (((ab(c)d)	(((abc	111000
  ((a(bc))d)	((a(bc	110100
  ((ab)(cd))	((ab(c	110010
  (a((bc)d))	(a((bc	101100
  (a(b(cd)))	(a(b(c	101010

  Tablonun 1.sütununda abcd çarpımının paranteze alınabilir biçimleri verilmiştir. İlk satırda yer alan (((ab(c)d) biçimini soldan sağa doğru okurken “)” parantezlerini görmezden gelerek 2.sütundaki (((abc dizilimini elde edebiliriz. Benzer biçimde ((a(bc))d) diziliminden ((a(bc elde edilecektir. Şimdi 2.sütundan bir dizilim alıp sonuna “d)” ekleyelim. Örneğin, 3.satırdaki ((ab(c dizilimi ile ((ab(cd) elde edilir. Soldan sağa doğru her bir ikili çarpımı “)” ile kapatırsak ((ab)(cd)) elde edilir. Dikkat ederseniz bu dizilim 1.sütundaki karşılığıdır.

  3.sütunun ne olduğu açık bir biçimde görülmektedir. “(“ sembollerini 1; a, b ve c harflerini de 0 sembolize etmektedir. O halde 1.sütunda yer alan her bir dizilime karşılık, 3 adet 1 ve 3 adet 0 içeren ve soldan sağa okunurken 0 sayısının 1 sayısından fazla olmadığı bir sayı dizisi karşılık gelmektedir. Bunların sayısının da ${b_3} = 5$ olduğu görülmektedir. O halde, genel olarak ${x_1}{x_2} \cdot \cdot \cdot {x_n}$ çarpımını ${b_{n - 1}}$ farklı biçimde paranteze alabilir.

• Şimdi, 1,2,3,4,5 ve 6 sayılarını 2 satır ve 3 sütundan oluşan bir tabloda (1) her bir satırda sayılar soldan sağa doğru okunurken küçükten büyüğe doğru dizili, (2) herhangi bir sütunda küçük sayı üstte olacak biçimde dizmeye çalışalım. Örneğin,

  1	2	4
  3	5	6

  Şimdi ilk satırda yer alan sayıları 1 ile ikinci satırda yer alan sayıları da 0 ile sembolize ederek tablodaki sayıların sırasına göre bir dizilim yaparsak $123456 \leftrightarrow 110100$ elde ederiz. Şimdi tam tersi 0 sayısının 1 sayısını soldan sağa geçmediği rastgele bir dizilimi ele alıp tablo oluşturalım. Örneğin, $101100 \leftrightarrow 123456$ ile

  1	3	4
  2	5	6

  elde edilir ki istenilen koşullara uygun bir tablomuz olur. O halde bu sorunun cevabı da ${b_3} = 5$ olacaktır.