Soru
\(k\) bir pozitif tam sayı olmak üzere, \[\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \left( {\begin{array}{*{20}{c}}{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}\] olduğunu gösteriniz.
Kaynak: IB High Level Paper 1 2013 Aralık (Sabah) Soru 12 (Sorunun son aşamasında istenen genellemedir. Soru doğrudan doğruya bu ispatla başlamamaktadır. Bu kadar zor sanmayın:) )
Çözüm
$z = \cos x + i \cdot \sin x$ için ${z^{ - 1}} = \cos (x) - i \cdot \sin (x)$ olacağından, \[z + {z^{ - 1}} = 2{\mathop{\rm cosx}\nolimits} \] dir. Bu durumda, \[{(z + {z^{ - 1}})^{2k}} = {2^{2k}} \cdot {\cos ^{2k}}x \quad (1)\] olur. Öte yandan sol tarafa binom açılımı uygulanırsa, \[{(z + {z^{ - 1}})^{2k}} = \sum\limits_{r = 0}^{2k} {\left( {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right){z^{2k - r}} \cdot {z^{ - r}}} \right)} = \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right){z^{2(k - r)}}} \quad (2)\] dir.
Bu ifadede, ${z^{2(k - r)}} = \cos \left( {2(k - r)x} \right) + i \cdot \sin \left( {2(k - r)x} \right)$ dikkate alınır ve $(1)$ ve $(2)$ birlikte düşünülürse, \[{2^{2k}} \cdot {\cos ^{2k}}x = \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\cos \left( {2(k - r)x} \right)} + i \cdot \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\sin \left( {2(k - r)x} \right)} \] olur. Karmaşık sayıların eşitliği gereği, sol tarafta sanal kısım olmadığından, $\sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\sin \left( {2(k - r)x} \right)} = 0$ dır.
Böylece, \[{2^{2k}} \cdot {\cos ^{2k}}x = \sum\limits_{r = 0}^{2k} {\left( {\begin{array}{*{20}{c}}
{2k}\\
r
\end{array}} \right)\cos \left( {2(k - r)x} \right)} \quad (3) \] olur. Dikkat edilirse $k \ne r$ için, \[\int\limits_0^{\frac{\pi }{2}} {\cos (2(k - r) \cdot x)} dx = \left. {\left( {\frac{1}{{2(k - r)}}\sin (2(k - r) \cdot x)} \right)} \right|_0^{\frac{\pi }{2}} = 0 \quad (4)\] dir.
$k = r$ için ise, \[\int\limits_0^{\frac{\pi }{2}} {\cos (2(k - r) \cdot x)} dx = \int\limits_0^{\frac{\pi }{2}} {1 \cdot } dx = \frac{\pi }{2} \quad (5)\] dir.
Bu durumda, $(3)$ te her iki tarafın da $0$ dan $\dfrac{\pi }{2}$ ye integrali alınırsa, \[{2^{2k}} \cdot \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{2}\] elde edilir. Böylece, \[\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}\] bulunur.
Çözüm (Ayhan Yanağlıbaş)
Verilen önermenin ispatını tümevarım yöntemi ile gösterelim. \[D(k){\rm{ }} = {\rm{ }}\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}} \] olmak üzere,
\[\begin{align*}
D(1) & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^2}xdx} \\
& = \int\limits_0^{\frac{\pi }{2}} {\left( {\frac{{1 + \cos 2x}}{2}} \right)dx} \\
& = \left. {\left[ {\frac{x}{2} + \frac{{\sin 2x}}{4}} \right]} \right|_0^{\frac{\pi }{2}}\\
& = \frac{\pi }{4} = \left( {\begin{array}{*{20}{c}}
2\\
1
\end{array}} \right) \cdot \frac{\pi }{{{2^3}}}
\end{align*}\]
doğrudur. Şimdide, \[D(k) = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}} \quad (1) \] önermesinin doğruluğunu kabul edip, \[D(k + 1) = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k + 2}}xdx = \left( {\begin{array}{*{20}{c}}
{2k + 2}\\
{k + 1}
\end{array}} \right).\frac{\pi }{{{2^{2k + 3}}}}} \quad (2)\] önermesinin doğruluğunu gösterelim. Bunun için \[\int {{{\cos }^n}xdx = } \frac{1}{n}\sin x{\cos ^{n - 1}}x + \frac{{n - 1}}{n}\int {{{\cos }^{n - 2}}xdx}\] indirgeme formülünden yararlanacağız. Bu formüle göre, \[\begin{align*}
D(k + 1) & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k + 2}}xdx} \\
& = \overbrace {\left. {\left( {\frac{1}{{2k + 2}}\sin x{{\cos }^{(2k + 1)}}x} \right)} \right|_0^{\frac{\pi }{2}}}^U + \overbrace {\frac{{2k + 1}}{{2k + 2}} \cdot \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} }^V
\end{align*}\] yazılabilir. \[u = \left. {\left( {\frac{1}{{2k + 2}} \cdot \sin x{{\cos }^{(2k + 1)}}x} \right)} \right|_0^{\frac{\pi }{2}} = {\rm{ }}0\] olur. Ayrıca, $v$ ifadesinde $(1)$ numaralı eşitlik kullanılırsa, \[v = \frac{{2k + 1}}{{2k + 2}} \cdot \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} = \frac{{2k + 1}}{{2k + 2}} \cdot \left( {\begin{array}{*{20}{c}}
{2k}\\
{k}
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k+1}}}}\] dir. \[\begin{align*}
D(k + 1) & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k + 2}}xdx} \\
& = v\\
& = \dfrac{{2k + 1}}{{2k + 2}} \cdot \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \dfrac{\pi }{{{2^{2k + 1}}}}\\
& = \dfrac{{2k + 1}}{{2(k + 1)}} \cdot \dfrac{{(2k)!}}{{k!.k!}} \cdot \dfrac{\pi }{{{2^{2k + 1}}}}
\end{align*}\] eşitliği $\dfrac{{2k + 2}}{{2(k + 1)}}$ ile genişletirsek, \[\begin{align*}
D(k + 1) & = \dfrac{{2k + 2}}{{2(k + 1)}} \cdot \dfrac{{2k + 1}}{{2(k + 1)}} \cdot \dfrac{{(2k)!}}{{k!.k!}} \cdot \dfrac{\pi }{{{2^{2k + 1}}}}\\
& = \dfrac{{(2k + 2)!}}{{(k + 1)!(k + 1)!}} \cdot \dfrac{\pi }{{4 \cdot {2^{2k + 1}}}}\\
& = {\rm{ }}\left( {\begin{array}{*{20}{c}}
{2k + 2}\\
{k + 1}
\end{array}} \right) \cdot \dfrac{\pi }{{{2^{2k + 3}}}}
\end{align*}\] olur. Böylece (2) numaralı eşitlik doğrulanmış olur. Tümevarım gereği ispat tamamlanmıştır.
Çözüm (Adem Çil)
Verilen integral, \[\begin{align*}
{I_{2k}} & = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} \\
& = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x(1 - {{\sin }^2}x)dx} \\
& = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}xdx} - \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x{{\sin }^2}xdx} \\
& = {I_{2k - 2}} - \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x{{\sin }^2}xdx}
\end{align*}\] olur. \[\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x{{\sin }^2}xdx} = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k - 2}}x\sin x \cdot \sin xdx} \] yazılır ve \[u = \sin x \Rightarrow dx = \cos xdx\] \[dv = {\cos ^{2k - 2}}x\sin xdx \Rightarrow v = - \frac{1}{{2k - 1}}{\cos ^{2k - 1}}x\] ile kısmi integral alınırsa, \[\begin{align*}
{I_{2k}} & = {I_{2k - 2}} - \left[ {\left. {\left( {\frac{1}{{2k - 1}}{{\cos }^{2k - 1}}x\sin x} \right)} \right|_0^{\frac{\pi }{2}} + \frac{1}{{2k - 1}}\int\limits_0^{\frac{\pi }{2}} {{{\cos }^{2k}}xdx} } \right]\\
& = {I_{2k - 2}} - \frac{1}{{2k - 1}} \cdot {I_{2k}}
\end{align*}\] olur. Bu eşitlikten, ${I_{2k}} = \left( {\frac{{2k - 1}}{{2k}}} \right) \cdot {I_{2k - 2}}$ indirgemesine ulaşırız. O halde, \[{I_{2k}} = \frac{{2k - 1}}{{2k}} \cdot \frac{{2k - 3}}{{2k - 2}} \cdot \cdot \cdot \frac{3}{4} \cdot {I_2}\] olur. ${I_2} = \int\limits_0^{\frac{\pi }{2}} {{{\cos }^2}xdx} = \frac{\pi }{4}$ yerine yazılırsa, \[{I_{2k}} = \frac{{2k - 1}}{{2k}} \cdot \frac{{2k - 3}}{{2k - 2}} \cdot \cdot \cdot \frac{3}{4} \cdot \frac{\pi }{4}\] olur. Payda 2 parantezine alınırsa, \[\begin{align*}
{I_{2k}} & = \frac{{2k - 1}}{k} \cdot \frac{{2k - 3}}{{k - 1}} \cdot \cdot \cdot \frac{3}{2} \cdot \frac{\pi }{{{2^{k + 1}}}}\\
& = \frac{{(2k - 1)(2k - 3) \cdot \cdot \cdot 3}}{{k!}} \cdot \frac{\pi }{{{2^{k + 1}}}} \end{align*}\] olur. Eşitliğin sağ tarafında pay ve paydayı $2k(2k - 2)(2k - 4) \cdot \cdot \cdot 2 = {2^k} \cdot k!$ ile çarparsak, \[\begin{align*}
{I_{2k}} & = \frac{{2k(2k - 1)(2k - 2)(2k - 3) \cdot \cdot \cdot 3 \cdot 2}}{{{2^k}k! \cdot k!}} \cdot \frac{\pi }{{{2^{k + 1}}}}\\
& = \frac{{(2k)!}}{{k! \cdot k!}} \cdot \frac{\pi }{{{2^{2k + 1}}}}\\
& = \left( {\begin{array}{*{20}{c}}
{2k}\\
k
\end{array}} \right) \cdot \frac{\pi }{{{2^{2k + 1}}}}
\end{align*}\] ile kanıt tamamlanır.
Soru

Şekilde, ABC üçgeninin kenarlarını ortak kenar kabul eden kareler çizilmiştir.
$\left| {JG} \right| = a$ birim, $\left| {HL} \right| = b$ birim ve $\left| {ON} \right| = c$ birim olduğuna göre, karelerin alanları toplamının
\[\frac{{{a^2} + {b^2} + {c^2}}}{3}\]
birim kare olduğunu gösteriniz.
Çözüm
13/01/2015 tarihinde verilecektir.
Soru
Düzgün sekizyüzlü biçimindeki bir labirentin herhangi bir köşesine bırakılan bir fare ayrıtlar üzerinde hareket ederek bırakıldığı bu köşenin karşı köşesine vardığında labirentten çıkmış oluyor. Farenin bir köşeden diğer bir köşeye gitme süresi $t$ saat olduğuna göre, labirentten ortalama çıkma süresini $t$ cinsinden bulunuz.(Soru metninde açık olsada tereddüte yer vermemek adına belirtmem gerekir ki, fare ilk bırakıldığı köşeye tekrar tekrar gelebilir, yani gittiği bir yoldan tekrar geri dönebilir.)
Çözüm
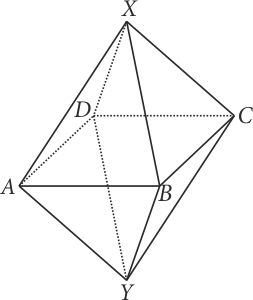
Şekildeki gibi bir sekizyüzlü düşünelim. Faremiz $X$ noktasına bırakılsın. Dolayısıyla $Y$ noktasına geldiğinde labirentten çıkmış olacaktır. Farenin $X$ noktasındayken labirentten ortalama çıkma (labirentten ortalama kurtulma) süresine $x$ diyelim. Benzer biçimde, fare $A$ noktasındayken labirentten ortalama çıkma süresine de $a$ diyelim. Dikkat edilirse, $B$, $C$ ve $D$ noktaları için de ortalama çıkma süresi $A$ noktası ile aynı yani $a$ olacaktır. Tekrar $X$ noktasına geri dönelim. Bu noktadan $\dfrac{1}{4}$ er ihtimalle $A$, $B$, $C$ ve $D$ noktalarına gidebilir. O halde, \[x = \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) = a + t\] dir. Eklenen $t$ süreleri $X$ den diğer noktalara geçmek için kullanılan ayrıtlardan kaynaklanmaktadır. Şimdi aynı mantıkta $A$ noktasını düşünelim.
- $\dfrac{1}{4}$ olasılıkla $B$ ye gidebilir. Ayrıtta geçen $t$ süre ve $B$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + t)$ olur.
- $\dfrac{1}{4}$ olasılıkla $D$ ye gidebilir. Ayrıtta geçen $t$ süre ve $D$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + t)$ olur.
- $\dfrac{1}{4}$ olasılıkla $X$ e gidebilir. Ayrıtta geçen $t$ süre ve $X$ den ortalama çıkma süresi eklenince: $\dfrac{1}{4}(a + 2t)$ olur.
- $\dfrac{1}{4}$ olasılıkla $Y$ ye gidebilir. Ayrıtta geçen $t$ süre eklenince: $\dfrac{1}{4}(t)$ olur.
O halde, $A$ noktasından ortalama çıkma süresi \[a = \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + t} \right) + \frac{1}{4}\left( {a + 2t} \right) + \frac{1}{4}t\] dir. Bu denklemden \[a = 5t\] bulunur. Böylece, \[x = a + t = 5t + t = 6t\] elde edilir.

