$\left( {\begin{array}{*{20}{c}} 5\\ 2 \end{array}} \right) = 10$ olduğunu görebiliriz. 

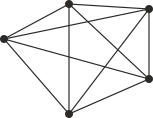
Köyler arasında kurulacak bir yol sistemini için bu yollardan herhangi biri ya seçilir ya da seçilmez. Yani her yol için 2 seçenek mevcuttur. O halde bu yollar ile toplamda  $${2^{10}}$$ farklı sistem kurulabilir. Bu değere ${S_0}$ diyelim. Böylece  $${S_0} = {2^{10}} = 1024$$ bulunur. Fakat tabii ki bu sistemler içinde istenilen şarta uygun olmayan durumlarda mevcuttur. Herhangi bir köyün izole olmadığı durumları saymak için aksini düşünüp köylerin izole olduğu durumları sayacak ve tüm durumdan çıkaracağız. 

Öncelikle şekildeki gibi köylerden sadece birinin izole olduğu durumların sayısını bulalım. 

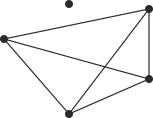
4 köy arasında 

$\left( {\begin{array}{*{20}{c}} 4\\ 2 \end{array}} \right)=6$ yol var. Bu nedenle seçilen bir köyün izole olduğu sistem sayısı  $${2^6}$$ olur. Şekildeki gibi 

$\left( {\begin{array}{*{20}{c}} 5\\ 1 \end{array}} \right) = 5$ farklı biçimde izole olacak köy seçebileceğimizden, herhangi bir köyün izole olduğu sistem sayısı 

$$\left( {\begin{array}{*{20}{c}} 5\\ 1 \end{array}} \right) \cdot {2^6}$$ olur. Bu değere ${S_1}$ diyelim. Böylece  $${S_1} = 5 \cdot 64 = 320$$ bulunur. 

Şimdi aşağıdaki şekildeki gibi iki köyün izole olduğu sistem sayısını bulalım. 

3 köy arasında şekilden de görüleceği üzere 

$\left( {\begin{array}{*{20}{c}} 3\\ 2 \end{array}} \right) = 3$ adet yol vardır. O nedenle bu yollar ile  $${2^3}$$ farklı sistem yapılabilir. Şekildeki gibi 2 köyün izole olduğu

$\left( {\begin{array}{*{20}{c}} 5\\ 2 \end{array}} \right)$ farklı seçim mümkün olduğundan, herhangi 2 köyün izole olduğu 

$$\left( {\begin{array}{*{20}{c}} 5\\ 2 \end{array}} \right) \cdot {2^3}$$ sistem vardır. Bu değere ${S_2}$ dersek,  $${S_2} = 10 \cdot 8 = 80$$ bulunur. 

Şimdi de 3 köyün izole olduğu durumların sayısını düşünelim. Kalan 2 köy arasında bir yol olacağından  $${2^1}$$ farklı sistem kurulabilir. Ayrıca 5 köy arasından 3 izole köy 

$\left( {\begin{array}{*{20}{c}} 5\\ 3 \end{array}} \right)$ farklı biçimde seçilebileceğinden, herhangi 3 köyün izole olduğu sistem sayısı 

$$\left( {\begin{array}{*{20}{c}} 5\\ 3 \end{array}} \right) \cdot 2$$ olur. Bu değere ${S_3}$ dersek,  $${S_3} = 10 \cdot 2 = 20$$ olur. 

Şimdi, 4 köyün izole olduğu durum sayısını düşünelim. Geriye kalan köy için herhangi bir yol çizilemeyeceğinden böyle bir seçimde 1 sistem oluşur. Herhangi 4 köyün izole olduğu 

$\left( {\begin{array}{*{20}{c}} 5\\ 4 \end{array}} \right) = 5$ seçim olacağından, bu durum kendini 5 kez tekrar eder. Bu değere de ${S_4}$ dersek,  $${S_4} = 5$$ olur.

Son olarak tüm köylerin izole olduğu 1 durum vardır. Bu değere de ${S_5}$ dersek,  $${S_5} = 1$$ olur. 

O halde içerme dışarma prensibi gereği, herhangi bir köyün izole olmadığı sistem sayısı 

$$\begin{align*} S &={S_0} - {S_1} + {S_2} - {S_3} + {S_4}-{S_5}\\ &=1024 - 320 + 80 - 20 + 5-1\\ &=768 \end{align*}$$ bulunur.

• $n$ sayısının tek adette terim içeren ardışık tüm yazılımlarını, tamamı bir $a$ tam sayısı ve negatif olmayan bir $b$ tam sayısı ile $n = \left( {a - b} \right) + ... + a + ... + \left( {a + b} \right)$ yani $n = a\left( {2b + 1} \right)$ biçiminde gösterebiliriz. $b$ negatif olmadığından $2b+1>0$ tek çarpanı, bu eşitliğin $n$ nin pozitif tek bölenleri kadar çözümü olacağını göstermektedir.
• $n$ sayının çift adette terim içeren ardışık tüm yazılımlarını da bir $a$ tam sayısı ve bir $b$ pozitif tam sayısı ile $n = \left( {a - b + 1} \right) + ... + a + \left( {a + 1} \right) + ... + (a + b)$ yani $n = \left( {a + 1/2} \right).2b = \left( {2a + 1} \right)b$ biçiminde gösterebiliriz.  $b$ ve $n$ pozitif olduğundan $2a+1>0$ olmalıdır. Bu nedenle bu eşitliğin de $n$ nin pozitif tek bölenleri kadar çözümü olacağı görülmektedir.

Kaynak: http://www.qbyte.org/puzzles/puzzle10.html  (soru 92)