Bu yazımda olasılık konusunun popüler sorularından birinin literatürdeki en güzel çözümünü verip sorunun daha özel iki durumunu ekleyeceğim (Çalışmanın PDF sürümü sayfanın bitimindedir).
Öncelikle literatürdeki bu soruya bir göz atalım.

Bu soruya vereceğim çözümün kime ait olduğunu bilmiyorum. Fakat inanılmaz derecede zekice bir çözüm olduğunu söylemek gerekiyor.
Çözüme geçmeden önce Viviani Teoremi nden bahsetmemiz gerekiyor.

Viviani Teoremi: Bir eşkenar üçgenin iç bölgesinde alınan her hangi bir \(P\) noktasından kenarlarına çizilen dikmelerin uzunlukları toplamı eşkenar üçgenin yüksekliğine eşittir.
Kanıt:

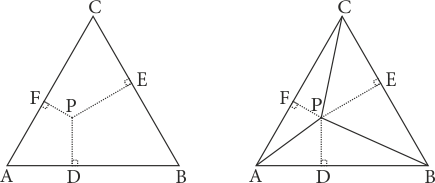
Şekillerdeki gibi bir kenari \(a\) birim olan bir \(ABC\) eşkenar üçgeni ve iç bölgesinde bir \(P\) noktası alalım. Soldaki şekilde olduğu üzere dikmeler \([PD]\), \([PE]\) ve \([PF]\) çizilsin. Sağdaki şekilde olduğu gibi \(P\) noktası ile köşeleri birleştirelim. Böylece \[|APB| = \frac{{a \cdot |PD|}}{2}\quad |BPC| = \frac{{a \cdot |PE|}}{2} \quad |APC| = \frac{{a \cdot |PF|}}{2} \] olur. Bu üçgenlerin alanları toplamının \(ABC\) üçgeninin alanına eşit olacağını bildiğimize göre (ABC üçgeninin yüksekliğine h dersek), \[|ABC| = |APB| + |BPC| + |APC|\] \[\frac{{a \cdot h}}{2} = \frac{a}{2} \cdot \left( {|PD| + |PE| + |PF|} \right)\] \[h = |PD| + |PE| + |PF|\] ile kanıt tamamlanır.

Muhtemelen bu teoreme neden ihtiyaç duyduğumuzu anlamış olmalısınız. Yapmamız gereken şey, çubuğu eşkenar üçgenin yüksekliğinin ve kırılan çubuğun parçalarını da P noktasından çizilen dikmelerin temsil ettiğini düşünmek olacaktır. Böylece P noktası değiştikçe kırılan parçalar biçimlenirken çubuğun kendisi bu parçalardan oluşmaya devam edecektir.
Temel üçgen eşitsizliği gereği biliyoruz ki bir üçgenin iki kenarının uzunlukları toplamı üçüncü kenarın uzunluğundan büyük olmalıdır. Bu nedenle kırılan parçalardan herhangi birinin uzunluğunun çubuğun yarısından fazla olmaması gerekir. Eğer herhangi bir parçanın uzunluğu çubuğun yarısından büyük olursa, diğer iki parçanın uzunlukları toplamının bu parçanın uzunluğundan küçük olacağı açıktır. Bu da demek oluyor ki inilen dikmelerin her birinin uzunluğu yüksekliğin yarısından fazla olmamalıdır. Yani, \(|PD| < \dfrac{h}{2}\), \(|PE| < \dfrac{h}{2}\) ve \(|PF| < \dfrac{h}{2}\) olmalıdır. 

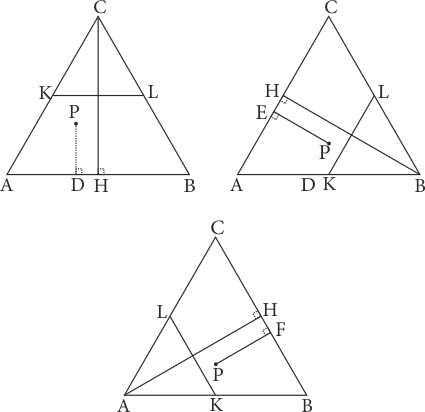
Yukarıdaki şekillerde \([KL]\) orta taban olarak çizilmiştir. Böylece, ilk şekilde \(|PD| < \dfrac{h}{2}\) olabilmesi için \(P\) noktasının \([KL]\) orta tabanı ile \([AB]\) arasında kalan bölgede yer alması gerektiği görülebilir. Aynı koşul diğer iki şekilde de mevcuttur. O halde her üç dikme uzunluğunun, yüksekliğin yarısından küçük olması için, \(P\) noktasının, aşağıdaki şekildeki gibi, \(ABC\) üçgeninin orta üçgeni içinde yer alması gerekir.

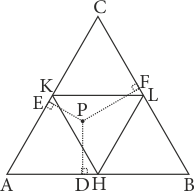
Böylece istenilen olasılık \[P = \frac{{|KLH|}}{{|ABC|}} = \frac{1}{4}\] olur.

Aşağıdaki interaktif şekilde \(P\) noktasını hareket ettirerek sağ tarafta dikmelerin oluşturduğu üçgenleri gözlemleyebilirsiniz.

Şimdi sorumuzu biraz daha geliştirebiliriz.

Öncelikle sentetik olarak incelediğimiz ilk çözümdeki eşkenar üçgeni \(H\) noktası başlangıç ve \(AB\) doğrusu \(x\) ekseni olacak biçimde şekildeki gibi koordinat düzlemine taşıyalım.

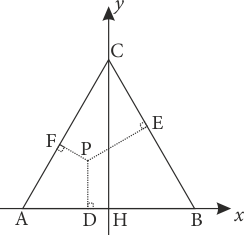
Eşkenar üçgenin bir kenar uzunluğuna \(2a\) birim diyelim. Bu durumda \[AC:\sqrt 3 (x+a) - y = 0\] ve \[BC:\sqrt 3 (x - a) + y = 0\] olacaktır. Öncelikle \(P\) noktasının dik üçgen oluşturması için bulunması gereken geometrik yerini tespit edelim. Bunun için oluşacak dik üçgenin dik kenarlarının \([PE]\) ve \([PF]\) olduğunu varsayalım. Tabii ki dik kenarlar \([PE]\) ile \([PD]\) veya \([PD]\) ile \([PF]\) de olacaktır. Ama biz başlangıçta birini inceleyip diğerlerinin genellemesine varmaya çalışacağız. Dik kenarlarımız \([PE]\) ve \([PF]\) olduğundan \[|PD{|^2} = |PE{|^2} + |PF{|^2}\] olmalıdır. \(P(x,y)\) noktasının \(AC\) e olan uzaklığı \[d(P,AC) = |PF| = \frac{{\left| {\sqrt 3 (x+a) - y} \right|}}{2}\] ve \(BC\) e olan uzaklığı \[d(P,BC) = |PE| = \frac{{\left| {\sqrt 3 (x - a) + y} \right|}}{2}\] olurken \(AB\) ye olan uzaklığı da \(|y|\) dir. Demek ki, \[\frac{{{{(\sqrt 3 (x + a) - y)}^2}}}{4} + \frac{{{{(\sqrt 3 (x - a) + y)}^2}}}{4} = {y^2}\] olmalıdır. Bu denklem düzenlenirse \[6{a^2} = {(y + \sqrt 3 a)^2} - 3{x^2}\] hiperbol denklemi elde edilir. Bu hiperbolün asal ekseninin \(y\) ekseni olduğuna dikkat edelim. Aşağıdaki şekilde hiperbolün eşkenar üçgen dahilinde ilgili parçası çizilmiştir.

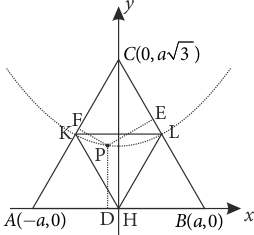
Dikkat ederseniz hiperbol \([AC]\) ve \([BC]\) yi orta noktalarında kesmektedir. Orta noktaları belirleyip denklemde yerine yazarsanız bunu daha net görebilirsiniz. Demek ki hiperbolün \(KL\) yayı üzerinde yer alan \(P\) noktaları için \([PE] \bot [PF]\) olacak biçimde, dikmeler bir dik üçgen belirtecektir.

Benzer biçimde \([PD] \bot [PF]\) ve \([PD] \bot [PE]\) koşullarına göre \(P\) noktalarının geometrik yerleri tespit edilirse aşağıdaki döndürülmüş hiperboller elde edilecektir. Aslında yukarıda bulduğumuz hiperbolün \(BK\) na göre simetriği soldaki hiperbolü; \(AL\) na göre simetriği ise sağdaki hiperbolü çizmektedir.

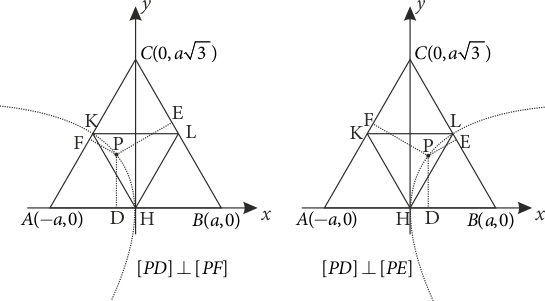
Dikkat edilirse, üç durum için oluşacak üçgenin dar açılı üçgen belirtmesi için \[|PE{|^2} + |PF{|^2} > |PD{|^2}\] \[|PD{|^2} + |PF{|^2} > |PE{|^2}\] \[|PD{|^2} + |PE{|^2} > |PF{|^2}\] eşitsizliklerinin sağlanması gerekecektir. Bu eşitsizlikler aşağıdaki bölgeyi gösterecektir.

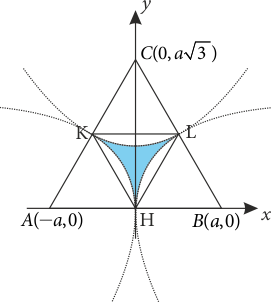
Tabii bu durumda geniş açılı üçgen belirtecek bölgede, orta üçgen içinde kalmak şartıyla, bu bölgenin dışındaki yerler olacaktır. Aşağıdaki interaktif şekilde \(P\) noktasını hareket ettirerek oluşan üçgenin açılarını inceleyebilirsiniz.

Geniş açılı üçgen oluşmasını sağlayan bölgenin alanını bulmak daha uygun olacaktır. Aşağıdaki şekilde üçgen içinde kalan hiperbol yayları ile üçgenin orta tabanları arasında kalan bölgeler eştir. Bu nedenle denklemini bulduğumuz hiperbolün \(KL\) yayı ile eşkenar üçgenin \([KL]\) orta tabanı arasında kalan bölgenin alanını bulup 3 ile çarpmamız, geniş açılı bölgenin alanını verecektir.

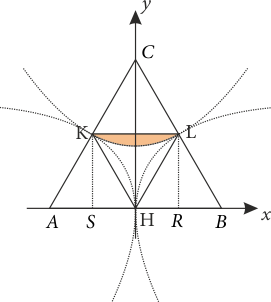
Bu bölgenin alanını bulmak için \(KLRS\) dikdörtgeninin alanından, hiperbolün \(S\) den \(R\) ye \(x\) ekseni ile arasında kalan alanı çıkarmamız gerektiği açıktır. Dikkat edilirse \(|KL|=a\) ve \(|RL|=\dfrac{{a\sqrt 3 }}{2}\) olurken \(S\left( { - \dfrac{a}{2},0} \right)\) ve \(R\left( { \dfrac{a}{2},0} \right)\) dir. Ayrıca hiperbol denkleminden \(y\) çekilirse, (\(y>0\) olduğundan) \[6{a^2} = {(y + \sqrt 3 a)^2} - 3{x^2} \Rightarrow y = \sqrt {6{a^2} + 3{x^2}}  - \sqrt 3 a\] olur. O halde şekildeki taralı bölgenin alanı \[|KLRS| - \int\limits_{ - \frac{a}{2}}^{\frac{a}{2}} {\left( {\sqrt {6{a^2} + 3{x^2}}  - \sqrt 3 a} \right)dx}  = \frac{{{a^2}\sqrt 3 }}{4}\left( {3 - \ln 16} \right)\] olur. Bu bölgeden 3 adet olduğundan geniş açılı bölgenin alanı \[\frac{{{a^2}3\sqrt 3 }}{4}\left( {3 - \ln 16} \right)\] bulunur. O halde dikmelerin geniş açılı üçgen belirtme olasılığı \[{P_{genis}} = \dfrac{{\dfrac{{{a^2}3\sqrt 3 }}{4}\left( {3 - \ln 16} \right)}}{{\dfrac{{4{a^2}\sqrt 3 }}{4}}} = \dfrac{{3 \cdot (3 - ln16)}}{4}\] olarak hesaplanır.

Parçaların dar açılı üçgen berirtme olasılığı ise üçgen belirtme olasılığından, geniş açılı üçgen belirtme olasılığının çıkarılmasıyla elde edilecektir. O halde \[{P_{dar}} = \frac{1}{4} - \frac{{3 \cdot (3 - ln16)}}{4} =  - 2 + 3\ln 2\] olarak bulunur.

Dar ve geniş açılı üçgenler için yapılan bu çalışma özgün bir çalışmadır. Lütfen kullanırken bunu göz önünde bulundurunuz.

Çalışmanın 20/02/2012 yılında yapılmış olan video anlatımı aşağıdadır.